A waiter at a restaurant gets a group's order completely wrong. Can you turn the table to get two or more orders right?

Problem statement
An arbitrary number of people are people sitting down, around a round table, waiting for their orders. When the waiter brings their orders, they mix everything up and no single person is served what they ordered.
Can you always turn the table so that at least two orders are correctly aligned? You can start by trying with the example in the figure above, assuming you are not colour-blind (sorry if you are :/).
Give it some thought...
Solvers
Congratulations to the ones that solved this problem correctly and, in particular, to the ones that submitted correct solutions:
- Attila K., Hungary;
- Filippo M., Italy;
- Luís S., Portugal;
- André S., Portugal.
(The list is in no particular order.)
Solution
I received some really interesting solutions and I'll be sharing a paraphrasing of the one I think is the most elegant.
Yes, it is always possible to turn the table some number of places in order to fix the dishes of at least two people at the same time. Let's see how to do it.
Each person sitting at the table will look to its left and count the number of plates until its own plate.
For example, if we consider this placement:

Then the corresponding numbers would be the following:
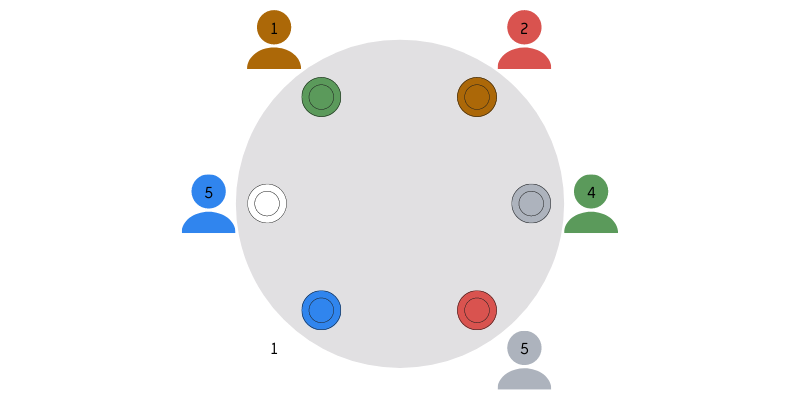
If there are \(n\) people sitting at the table, that number is an integer between \(1\) and \(n - 1\), inclusive. It is not \(0\) because that would mean that person got the correct plate and it is not \(n\) because that is a whole turn around the table, also meaning that person would've gotten its own plate.
We have seen that each person has a number inside the set
\[ \{ 1, 2, \cdots, n-1 \} ~~~,\]
and there are \(n\) people, but that set only contains \(n - 1\) distinct numbers. Therefore, the pigeonhole principle tells you that at least two persons have the same number \(d\), which means you can turn the table \(d\) times in the counter-clockwise direction to deliver the correct plate to them.
Don't forget to subscribe to the newsletter to get bi-weekly problems sent straight to your inbox and to add your reaction below.
Become a better Python 🐍 developer 🚀
+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!
My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.
