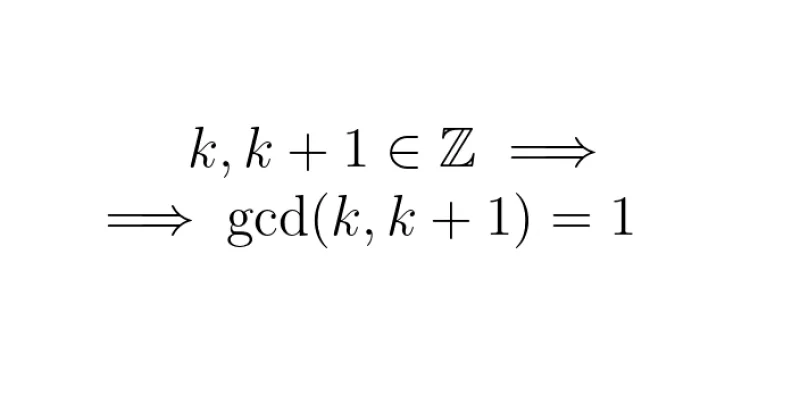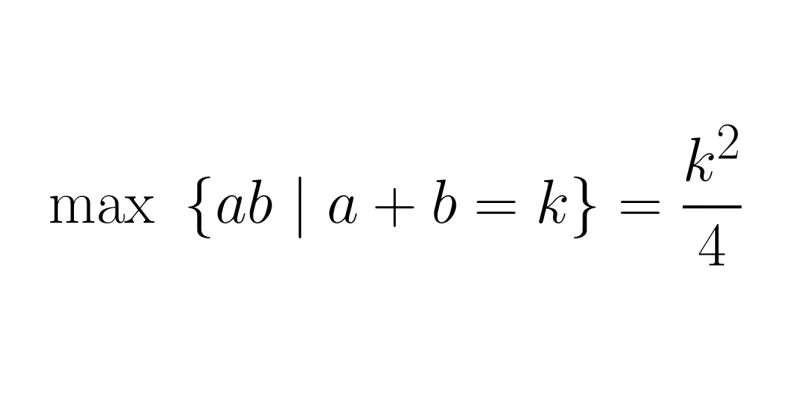Some people are standing quiet in a line, each person with a hat that has one of two colours. How many people can guess their colour correctly?
Join me in this blog post for Pokéfans and mathematicians alike. Together we'll find out how long it would take to fill your complete Pokédex by only performing random trades.
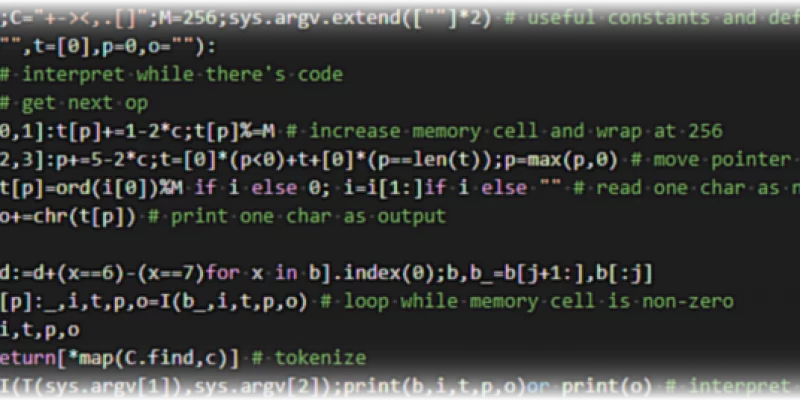
In this blog post I'll show you how you can write a full interpreter for the brainf*ck programming language in just 14 lines of Python. Be prepared, however, to see some unconventional Python code!
In this problem you have to devise a strategy to beat the computer in a "guess the polynomial" game.
Let's prove that if \(k\) is an integer, then \(\gcd(k, k+1) = 1\). That is, any two consecutive integers are coprime.
Let's prove that if you want to maximise \(ab\) with \(a + b\) equal to a constant value \(k\), then you want \(a = b = \frac{k}{2}\).
This simple problem is an example of a very interesting phenomenon: if you have a large enough "universe" to consider, even randomly picked parts exhibit structured properties.