Let's prove that there are two irrational numbers, call them \(a\) and \(b\), such that \(a^b\) is a rational number! And let's do it in a tweet.
Follow me on Twitter, where I write about Python, APL, and maths.
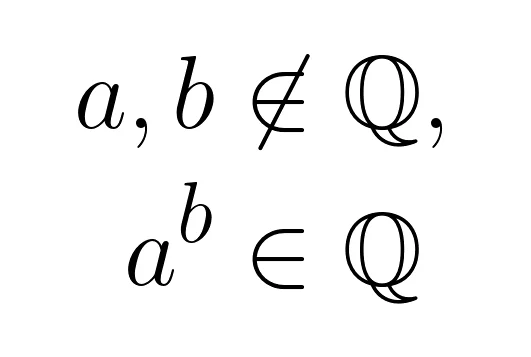
Twitter proof
Twitter proof:
— Mathspp (@mathsppblog) July 23, 2020
Let a=b=√2. If a^b is rational then there is nothing to be done. Assume a^b is irrational. Redefine a=√2^√2. Notice how a^b = (√2^√2)^√2 = (√2)^2 = 2 which is clearly rational. QED.https://t.co/3sFinyzJwu
Do you have an idea for a twitter proof? Let me know in the comments below!
I hope you learned something new! If you did, consider following the footsteps of the readers who bought me a slice of pizza 🍕. Your small contribution helps me produce this content for free and without spamming you with annoying ads.
