Let's prove that, if a set has size \(n\), then that same set has exactly \(2^n\) subsets.
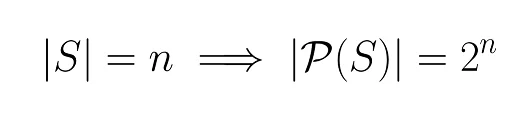
Twitter proof
Twitter proof:
— Mathspp (@mathsppblog) August 6, 2020
Take a set of size n. For any of its subsets, we can label items with 0/1 depending on whether or not the item is in the subset or not, and to any such labelling corresponds a single subset. There are 2^n such labellings, hence 2^n subsets.https://t.co/5uxKAi7D9T
Do you have an idea for a twitter proof? Let me know in the comments below!
Become a better Python 🐍 developer 🚀
+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!
My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.
