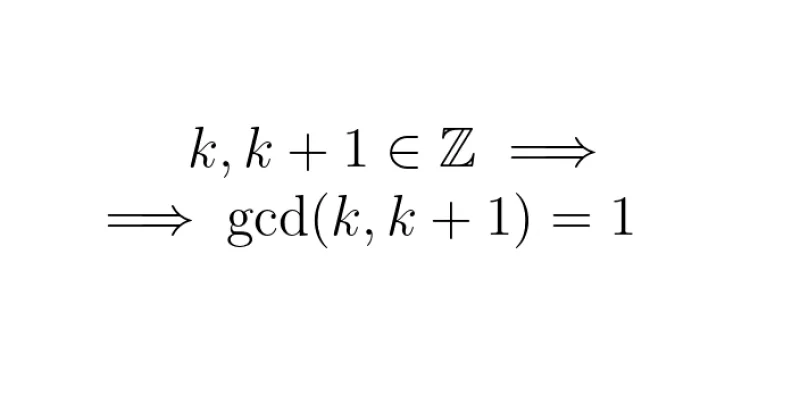Can you prove that there are arbitrarily many primes in arbitrarily big intervals?
Let's prove that if \(k\) is an integer, then \(\gcd(k, k+1) = 1\). That is, any two consecutive integers are coprime.
This simple problem is an example of a very interesting phenomenon: if you have a large enough "universe" to consider, even randomly picked parts exhibit structured properties.