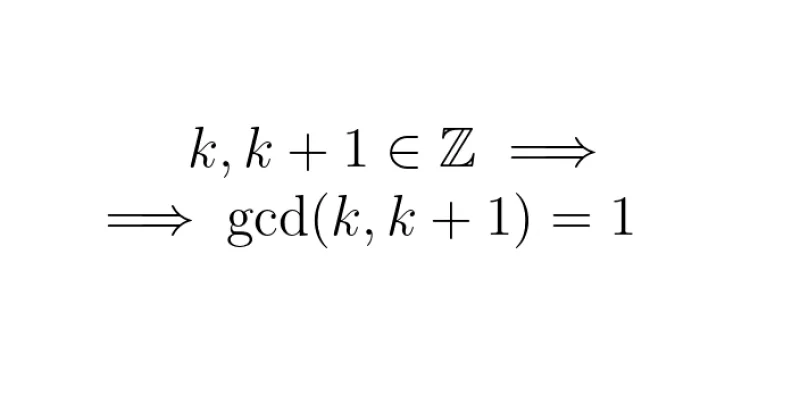Can you prove that there are arbitrarily many primes in arbitrarily big intervals?
In this problem you have to devise a strategy to beat the computer in a "guess the polynomial" game.
Let's prove that if \(k\) is an integer, then \(\gcd(k, k+1) = 1\). That is, any two consecutive integers are coprime.
This simple problem is an example of a very interesting phenomenon: if you have a large enough "universe" to consider, even randomly picked parts exhibit structured properties.
Split the numbers 0, 1, ..., 15 into two sets with sum interesting properties!
Can you measure exactly \(2\)L of water with two plain buckets with volumes of \(14\)L and \(5\)L? Of course you can!
Two friends were bored and decided to play a game... a mathematical game with a paper bag!
Here's how I like to solve my equations: just walk around randomly until I trip over a solution!