I have always liked the concept of fractal. They are very beautiful, they have a notion of infinity embedded in them, and they make no sense (seriously though, self-similarity?). How could they not be loved?

Fractals and the Mandelbrot set

Despite being fond of fractals, I had never understood them because I didn't know how to mathematically define one. I knew how to draw some, for example the snowflake or the Sierpinski triangle, but drawing a fractal and mathematically defining it aren't quite the same thing...

Enlightenment struck after watching this video from Numberphile about the Mandelbrot set, the fractal I presented above. After all, a fractal like this was not but a simple formula and a check for a bound on a sequence! I recommend to all of you that you watch that video.

To decide if a complex number \(c\) belongs to the fractal or not, you define \(f(x) = x^2 + c\) and then you look at the sequence \(c, f(c), f(f(c)), f(f(f(c))), ...\). If the absolute value of these numbers stays bounded, then \(c\) belongs to the Mandelbrot set. If these numbers keep on growing in absolute value, then \(c\) does not belong to the set.

After learning how to create the Mandelbrot set I put that knowledge to practice, making use of Python.

The script below uses pygame to create a simple rendering of the Mandelbrot set. The image will be black and white and you need to use Ctrl + C to stop the script after you're done looking at the image.

import pygame

WIDTH = HEIGHT = 400

screen = pygame.display.set_mode((WIDTH, HEIGHT))

def f(z, c):
    return z**2 + c

MAX_ITER = 50
for x in range(WIDTH):
    for y in range(HEIGHT):
        re = 3 * x / WIDTH - 2.3
        im = 3 * y / HEIGHT - 1.5
        z = c = complex(re, im)
        iter = 0
        while iter < MAX_ITER and abs(z) < 2:
            z = f(z, c)
            iter += 1

        if abs(z) < 2:
            screen.set_at((x, y), pygame.Color(0, 0, 0))
        else:
            screen.set_at((x, y), pygame.Color(255, 255, 255))

pygame.display.flip()
pygame.image.save(screen, "bw.png")

while True:
    for ev in pygame.event.get():
        pass

This will open said pygame window and it will save an image bw.png with the rendering:

To make this slightly more interesting, we can create a list with shades of gray and assign each shade to an iteration number, so that the colour a pixel is coloured in depends on how quickly the while loop was broken. To achieve this, we need to modify the middle section of the code:

# We added this.
GRAYS = list(
    reversed(
        [pygame.Color(*(int(255 * i / MAX_ITER),) * 3) for i in range(MAX_ITER + 1)]
    )
)

for x in range(WIDTH):
    for y in range(HEIGHT):
        re = 3 * x / WIDTH - 2.3
        im = 3 * y / HEIGHT - 1.5
        z = c = complex(re, im)
        iter = 0
        while iter < MAX_ITER and abs(z) < 2:
            z = f(z, c)
            iter += 1

        screen.set_at((x, y), GRAYS[iter])  # <-- Modified here.

pygame.image.save(screen, "gray.png")  # <-- Save with a new name.

This produces the following rendering:

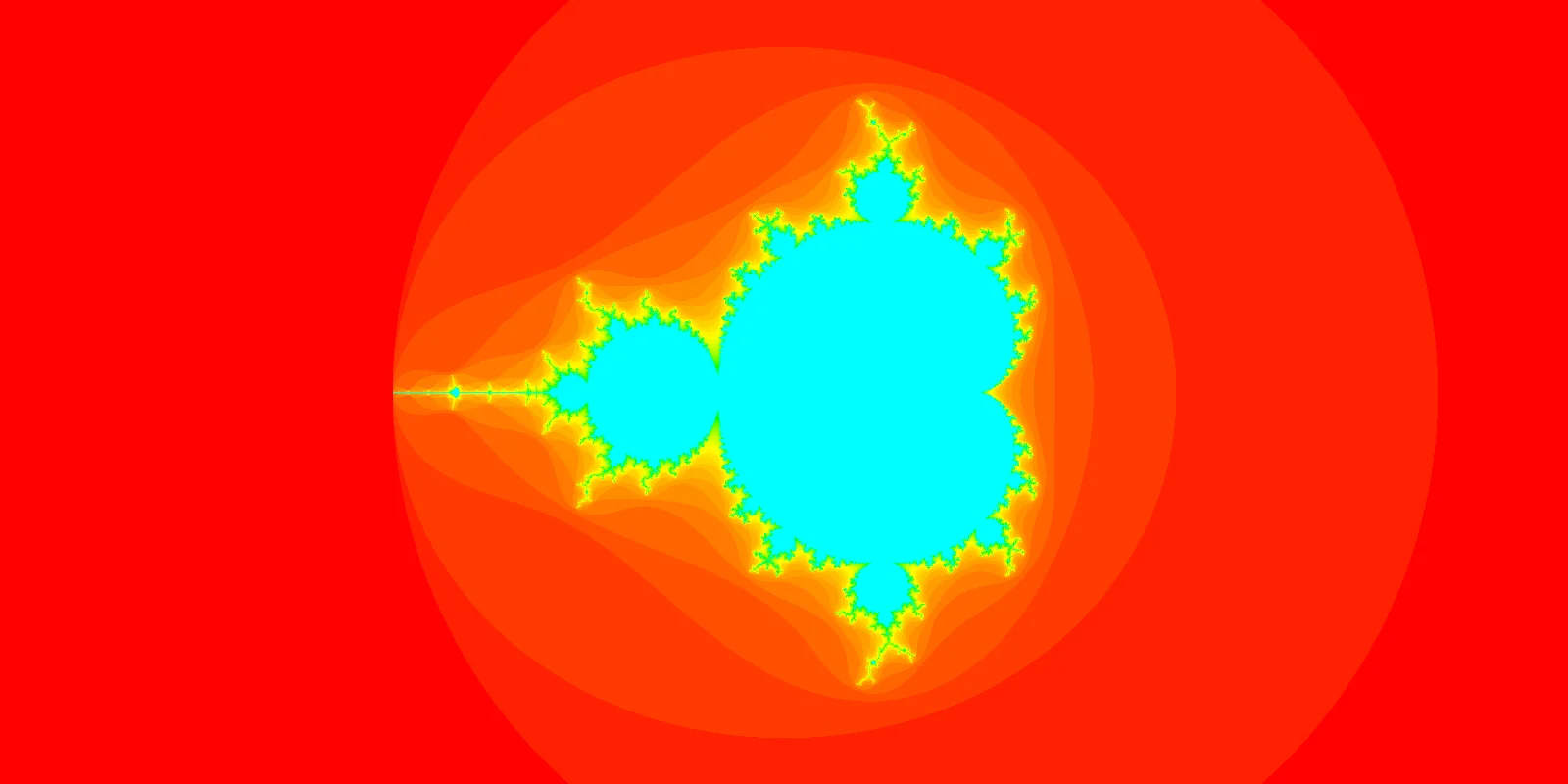
To make this even more colourful, we can do all sorts of crazy things. I played around with lots of lists of colours and I ended up finding this one that I like:

colours = []
for i in range(MAX_ITER + 1):
    c = pygame.Color(0, 0, 0)  # Irrelevant RGB values.
    c.hsla = (180 * (i / MAX_ITER) ** 0.8, 100, 50, 100)
    colours.append(c)

This palette produces the much more colourful version you can find below:

Here is the full code, with the dimensions used to generate the thumbnail for this article:

import pygame

WIDTH = 1600
HEIGHT = 800

screen = pygame.display.set_mode((WIDTH, HEIGHT))

def f(z, c):
    return z**2 + c

MAX_ITER = 50

# GRAYS = list(
#     reversed(
#         [pygame.Color(*(int(255 * i / MAX_ITER),) * 3) for i in range(MAX_ITER + 1)]
#     )
# )

colours = []
for i in range(MAX_ITER + 1):
    c = pygame.Color(0, 0, 0)  # Create a colour instance.
    c.hsla = (180 * (i / MAX_ITER) ** 0.8, 100, 50, 100)
    colours.append(c)

for x in range(WIDTH):
    for y in range(HEIGHT):
        re = 6 * x / WIDTH - 3.5
        im = 3 * y / HEIGHT - 1.5
        z = c = complex(re, im)
        iter = 0
        while iter < MAX_ITER and abs(z) < 2:
            z = f(z, c)
            iter += 1

        screen.set_at((x, y), colours[iter])

pygame.display.flip()
pygame.image.save(screen, "thumbnail.png")

while True:
    for ev in pygame.event.get():
        pass

Next steps

There are plenty of things you can do if you want to keep exploring this world. Some ideas include:

• add zoom to your rendering when the user clicks;
• explore other colour paletters;
• look into producing high-definition renderings; and
• learn about the Julia set.

Become a better Python 🐍 developer 🚀

+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!

My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.