Let's prove that if you want to maximise \(ab\) with \(a + b\) equal to a constant value \(k\), then you want \(a = b = \frac{k}{2}\).
Twitter proof
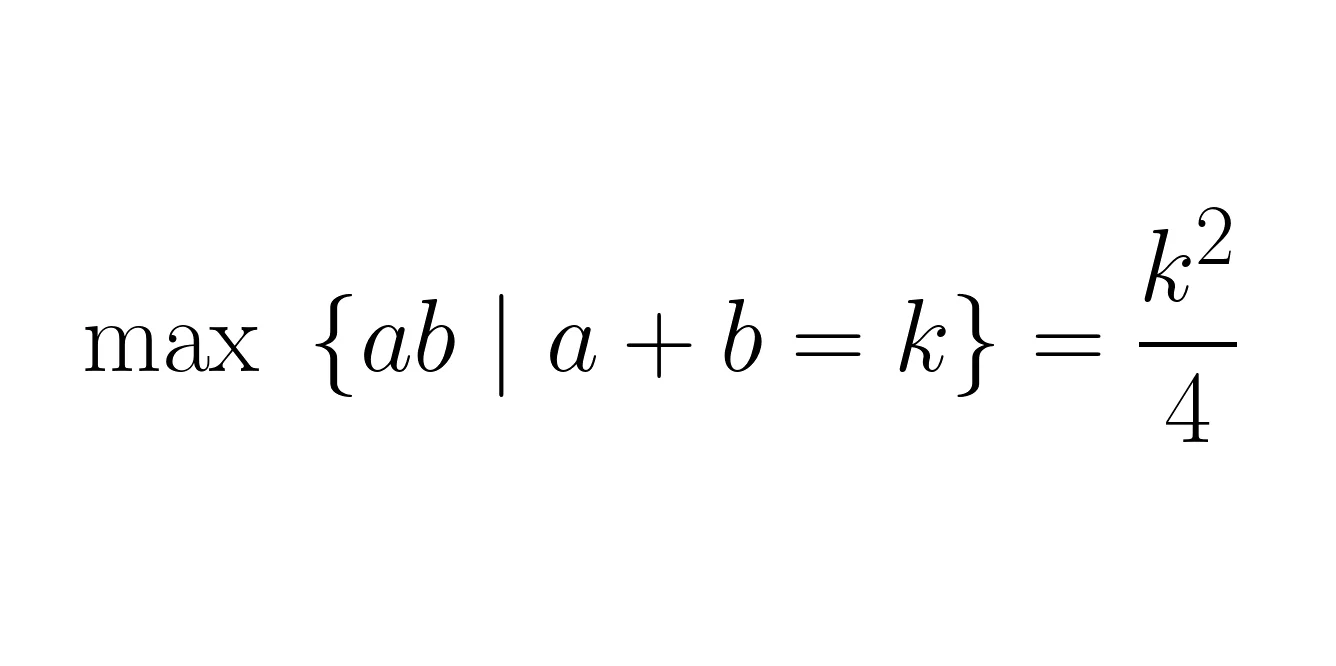
Twitter proof:
— Mathspp (@mathsppblog) November 5, 2020
Take s = k/2. If a = s+h then b = s-h, from which we get that ab = (s+h)(s-h) = s^2 - h^2. Because we know h^2 >= 0, ab is maximised when h = 0, that is a = b = s = k/2.https://t.co/9ypegSMF2F
Do you have an idea for a twitter proof? Let me know in the comments below!
Become a better Python 🐍 developer, drop by drop 💧
Get a daily drop of Python knowledge. A short, effective tip to start writing better Python code: more idiomatic, more effective, more efficient, with fewer bugs. Subscribe here.
