Given some paper squares, can you slice them and then glue them back together to form a single square?

Problem statement

Given \(n\) squares of side lengths \(a_1, a_2, \cdots, a_n\), is it possible to cut them in a way that the cut pieces can be rearranged into a single, larger square with no holes or no overlapping pieces?

You can actually try this out with paper squares and a pair of scissors!

Solution

The first step is to recognize it suffices to prove the statement for two squares. That is, given two squares of side lengths \(a\) and \(b\), it is always possible to cut them into pieces and rearrange those pieces to create a single square.

Let us start by considering the case where \(a > b\).

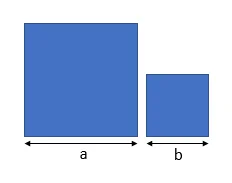
Take the bigger square and make a cut parallel to one of the sides in order to create two rectangles: one of dimensions \(a \times b\) and the other of dimensions \(a\times (a-b)\). Take the rectangle that is \(a \times b\) and cut it along the diagonal, getting two identical right triangles with sides \(a\) and \(b\).

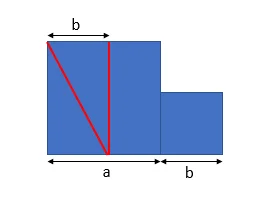
Cut the rectangle that is \(a \times (a-b)\) in order to obtain a square \((a-b) \times (a-b)\) and a rectangle \(b \times (a-b)\), putting it next to the smaller square (\(b \times b\)) to create a new rectangle \(b \times a\), which we cut along the diagonal.

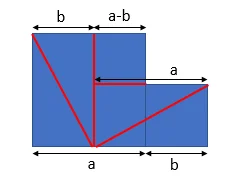
At this point, we have \(4\) right triangles of sides \(a\) and \(b\) and a square that is \((a-b) \times (a-b)\). All we need is to put the pieces together in a convenient way:

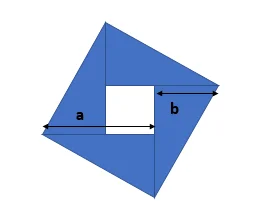
The hole that is missing is filled by the square \((a-b) \times (a-b)\) that hasn't been used.

Note that the side of the new square is \(\sqrt{a^2 + b^2}\), as expected: the sum of the areas of the two initial squares is \(a^2 + b^2\), meaning a square made out of those two would need to have sides of length \(\sqrt{a^2 + b^2}\).

In the beginning we assumed \(a > b\). If \(a = b\) we just need to cut the two squares along the diagonal and glue together the \(4\) right triangles. The case \(a < b\) can be handled similarly to the case \(a > b\) by swapping the two squares.

We have proved we can transform two squares into a single one by a succession of cuts and rearrangements. To prove this holds for a generic number of initial squares we proceed to prove the statement by complete induction. The base case, \(n = 2\), is done.

For the induction step, we suppose it is true for any number of squares between \(2\) and \(n\) and it becomes easy to check it works for \(n+1\) as well: start by cutting two squares to get one single square out of those two; we just got from \(n+1\) squares with side lengths \(a_1, a_2, \cdots, a_{n+1}\) to \(n\) squares with side lengths \(a_1, a_2, \cdots, a_{n-1}, a'\), with \(a' = \sqrt{a_n^2 + a_{n+1}^2}\). By the induction hypothesis we can cut the \(n\) remaining squares and then glue all the pieces back together to form a single square, thus concluding the induction step!

Become a better Python 🐍 developer 🚀

+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!

My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.