You are sunbathing when you decide to go and talk to some friends under a nearby sun umbrella, but first you want to get your feet wet in the water. What is the most efficient way to do this?

Problem statement

The problem statement is just like you read above. You are on the sand and need to go to another place on the sand, but first you need to go to the shoreline, which you can assume is a straight line:

How do you pick your path so that you walk as little as possible (because the sand is really hot!)?

If you need any clarification whatsoever, feel free to ask in the comment section below.

Solvers

Congratulations to the ones that solved this problem correctly and, in particular, to the ones who sent me their correct solutions:

• “Todi Liju”, Portugal;
• João F., Portugal;
• António, Portugal;
• David, Portugal;
• Eleonora, Portugal.

(The list is in no particular order.)

Solution

The easiest way to formulate the solution is as follows:

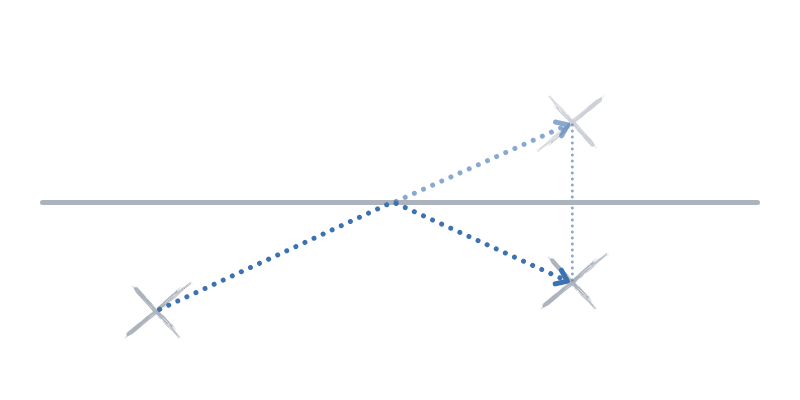
You just have to reflect one of the umbrellas to the other side of the shoreline, and then the shortest path between the reflection and the other umbrella is a straight line. This path crosses the shoreline, so it does what is needed. When you reach the shoreline, instead of walking into the ocean you turn around and keep walking in a straight line to the other umbrella.

This works because the distance from any point in the shoreline to an umbrella is the same as the distance from that same point to the umbrella reflected along the shoreline.

Don't forget to subscribe to the newsletter to get bi-weekly problems sent straight to your inbox and to add your reaction below.

Become a better Python 🐍 developer 🚀

+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!

My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.