Problems

Logic puzzles, riddles, & maths problems

Buy the book

Problem #066 – regex crossword

Can you solve this crossword where all hints are regular expressions?

mathematics regex
Problem #065 – clock synchronisation

When will these two clocks synchronise again?

mathematics
Problem #064 – infinite mathematicians with hats

How can an infinite number of mathematicians figure out their own hat colours?

logic mathematics sequences
Problem #063 – arbitrarily many primes in arbitrarily big intervals

Can you prove that there are arbitrarily many primes in arbitrarily big intervals?

logic mathematics number theory primes
Problem #062 – sliding coins

Can you align all of the coins on the right edge of the board?

invariants logic mathematics
Problem #061 – flower garden

Three mathematicians discuss a beautiful flower garden and the coloured flowers within.

logic mathematics
Problem #060 – realtor commissions

Two realtors discuss who's netting the award for highest average commission, but it isn't clear who the winner is...

logic mathematics
Problem #059 – marching pegs

How can you swap the coloured pegs if they can only march forward?

logic mathematics
Problem #058 – identifying light bulbs

Please help me identify these 100 light bulbs by turning ON and OFF their switches.

binary logic mathematics
Problem #057 – how to find the circle centre

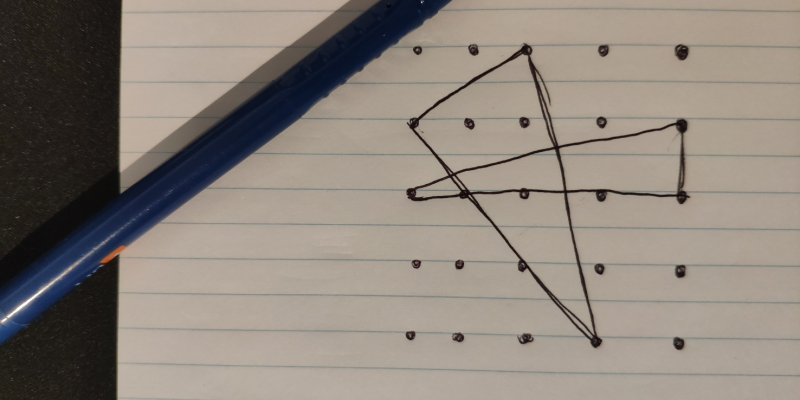
Can you find the centre of the circle with just five lines?

geometry mathematics
Problem #056 – tennis tournament

How many matches does it take to find the winner of a tennis tournament?

combinatorics mathematics
Problem #055 – horse racing

25 horses racing, and you have to find out the fastest ones!

logic mathematics
Problem #054 – imperfect compression

Can you show that perfect compression is impossible?

combinatorics induction mathematics pigeonhole principle
Problem #053 – weighing the odd one out

Can you find the fake ball by weighing it?

logic mathematics
Problem #052 – chessboard domino

Can you tile a chessboard with two missing squares?

chess combinatorics mathematics
Problem #051 – queens and knights

How many queens and knights can you place on a chessboard?

chess combinatorics mathematics
Problem #050 – 8 queens

In how many ways can you place 8 queens on a chessboard?

chess combinatorics mathematics
Problem #049 – coin pyramid

Can you make the pyramid point the other way by moving only three coins?

geometry mathematics
Problem #048 – trick or treat

Can you help these kids trick or treat their entire neighbourhood in this Halloween special?

combinatorics logic mathematics probability
Problem #046 – triangle grid

Can you draw 4 triangles in this 5 by 5 grid, covering all dots?

geometry mathematics