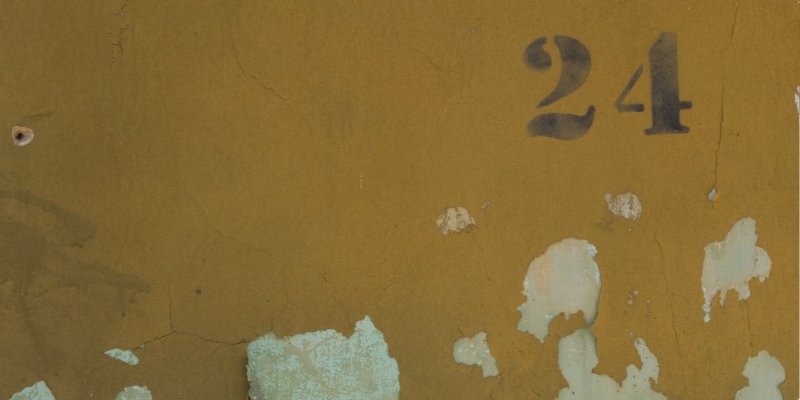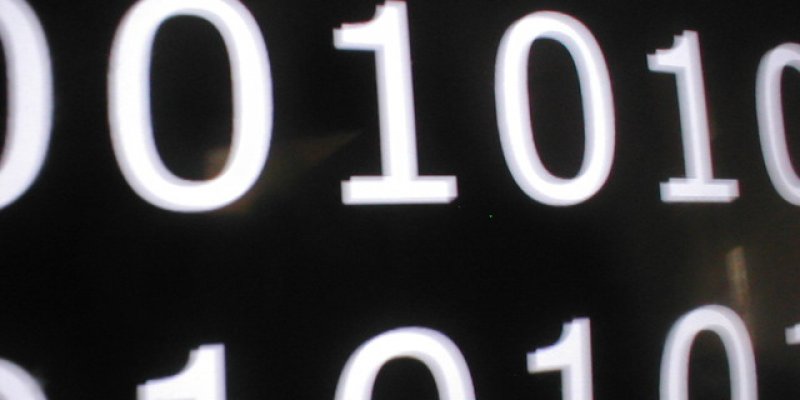In this problem you have to devise a strategy to beat the computer in a "guess the polynomial" game.
This simple problem is an example of a very interesting phenomenon: if you have a large enough "universe" to consider, even randomly picked parts exhibit structured properties.
Today we are visiting a specific instance of a well-known basic mathematics game, the 24 Game. The "24 Game" is usually played with younger students because it helps them develop skills related to the basic arithmetic operations.
Take out a piece of paper and a pencil, I am going to ask you to write some letters in your sheet of paper and then I am going to challenge you to fold the sheet of paper... with a twist!
\(n\) mathematicians with numbered party hats gather around in a circle... It is a matter of life or death!
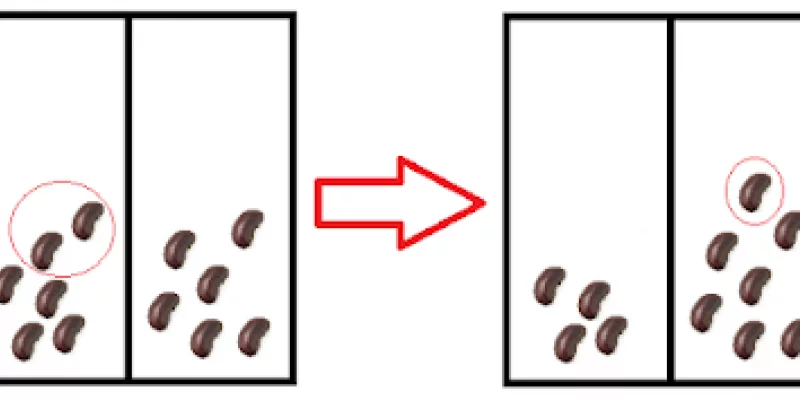
There's 100 drawers and 100 shuffled balls. Can you find the one I choose?
Can you cover all of the rational numbers in [0, 1] with tiny intervals?
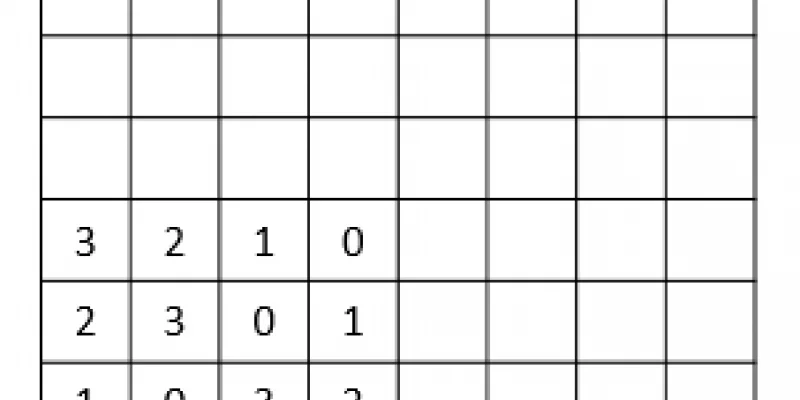
Split the numbers 0, 1, ..., 15 into two sets with sum interesting properties!
Given some paper squares, can you slice them and then glue them back together to form a single square?
Is it true that every integer you can think of has a multiple written out only with \(0\)s and \(1\)s?
I find the problem in this post rather fun to think about because it is a problem about a game that can actually be played between two players.
This problem is a really interesting problem I solved two times. The first time I solved it I failed to prove exactly how it works... then some years later I remembered the problem statement and was able to solve it properly. Let's see how you do!
In this post I talked about the riddle of the water buckets. Now I challenge you to prove that in some situations it is impossible to solve it!
Gandalf has some Hobbits to appease but his task seems to go on forever. Can you give him a hand..?
