Let's prove that, if a set has size \(n\), then that same set has exactly \(2^n\) subsets.
Twitter proof
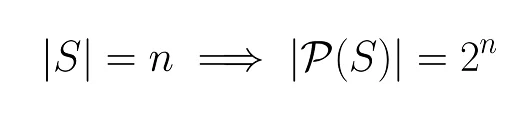
Twitter proof:
— Mathspp (@mathsppblog) August 6, 2020
Take a set of size n. For any of its subsets, we can label items with 0/1 depending on whether or not the item is in the subset or not, and to any such labelling corresponds a single subset. There are 2^n such labellings, hence 2^n subsets.https://t.co/5uxKAi7D9T
Do you have an idea for a twitter proof? Let me know in the comments below!
Become a better Python 🐍 developer, drop by drop 💧
Get a daily drop of Python knowledge. A short, effective tip to start writing better Python code: more idiomatic, more effective, more efficient, with fewer bugs. Subscribe here.
