Today I learned that the length of the terms of the “look-and-say” sequence has a well-defined growth rate.

What is the look-and-say sequence?

The look-and-say sequence is a numerical sequence that starts with 1, 11, 21, 1211, 111221. Can you guess what the next term is?

Each consecutive term comes from “reading out” the contents of the previous term. So, looking at 111221, we can split it into groups: 111, 22, and 1. Then, we read out each group:

• three 1s;
• two 2s; and
• one 1.

So, the next term is 312211. And the next:

• one 3;
• one 1;
• two 2s; and
• two 1s.

So, the next term would be 13112221.

Conway's Constant

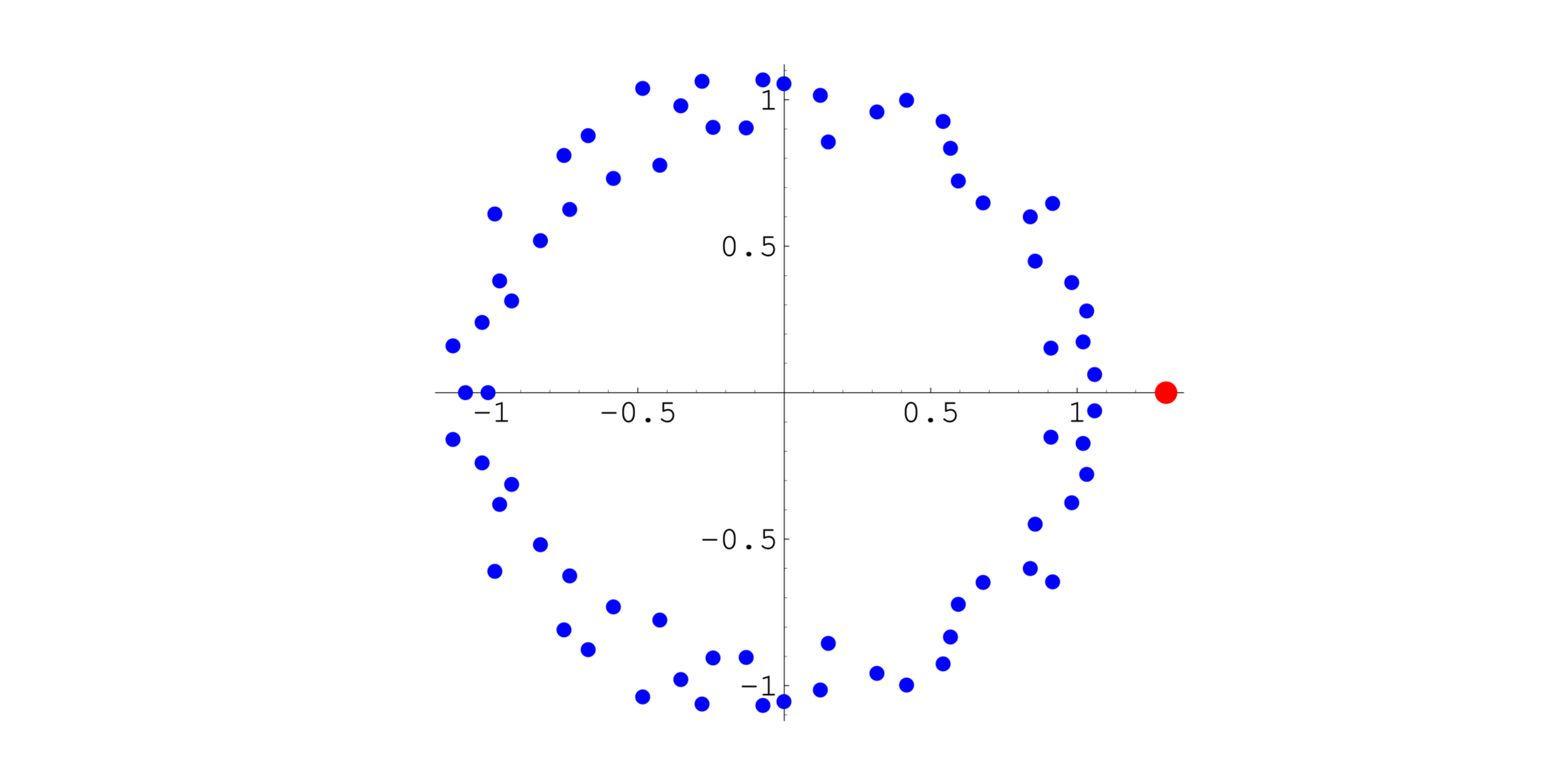
What I just learned is that the length of the next term is, on average, \(1.303577269\cdots\) times larger than the length of the previous term. Rounding it down, it means that terms grow by about \(30\%\) each iteration.

It was John Conway that proved that the ratio of the lengths of two consecutive terms converged to that value, and that value is now called Conway's Constant.

If you are wondering where that number came from, it's the only positive real root of the following polynomial:

\[ \begin{alignat}{9} &+x^{71} & &-x^{69} &-2 x^{68} &-x^{67} &+2 x^{66} &+2 x^{65} &+x^{64} &-x^{63} \\ &-x^{62} &-x^{61} &-x^{60} &-x^{59} &+2 x^{58} &+5 x^{57} &+3 x^{56} &-2 x^{55} &-10 x^{54} \\ &-3 x^{53} &-2 x^{52} &+6 x^{51} &+6 x^{50} &+x^{49} &+9 x^{48} &-3 x^{47} &-7 x^{46} &-8 x^{45} \\ &-8 x^{44} &+10 x^{43} &+6 x^{42} &+8 x^{41} &-5 x^{40} &-12 x^{39} &+7 x^{38} &-7 x^{37} &+7 x^{36} \\ &+x^{35} &-3 x^{34} &+10 x^{33} &+x^{32} &-6 x^{31} &-2 x^{30} &-10 x^{29} &-3 x^{28} &+2 x^{27} \\ &+9 x^{26} &-3 x^{25} &+14 x^{24} &-8 x^{23} & &-7 x^{21} &+9 x^{20} &+3 x^{19} &-4 x^{18} \\ &-10 x^{17} &-7 x^{16} &+12 x^{15} &+7 x^{14} &+2 x^{13} &-12 x^{12} &-4 x^{11} &-2 x^{10} &+5 x^9 \\ &&+x^7 &-7 x^6 &+7 x^5 &-4 x^4 &+12 x^3 &-6 x^2 &+3 x &-6 \end{alignat}\]

Now, where does that polynomial come from? I have no idea!

What I find the most interesting is that we have this sequence that seems to be unrelated to maths, given that the way in which you build the successive terms is through a word game, this sequence does exhibit some nice behaviour that maths can explain!

Isn't that cool?!

You can read a bit more about this sequence and variations in this article.

That's it for now! Stay tuned and I'll see you around!

Become a better Python 🐍 developer 🚀

+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!

My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.

References

• Look-and-Say Numbers (feat John Conway) - Numberphile, YouTube, https://www.youtube.com/watch?v=ea7lJkEhytA [last accessed 15-03-2022];
• Weisstein, Eric W. “Conway's Constant.” From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/ConwaysConstant.html [last accessed 16-03-2022];