The third article of this short series concerns itself with the implementation of the backpropagation algorithm, the usual choice of algorithm used to enable a neural network to learn.

Purpose of this article

In this article we will be deriving and implementing the backpropagation algorithm. That is, we will be performing the necessary calculations in order to see how the algorithm works, and then we will implement it. After the algorithm is implemented, we will run a small test to verify empirically that it is working.

Preamble

I will try my best to write an intuitive explanation of what really happens under the hood, and at the same time I will include all the mathematics needed to formalise what is really going on. If I succeed, you will be able to grasp what is going on by reading the intuitive explanations and you will be able to check I didn't make any mistakes if you check the mathematics.

First things first, we need to understand why we need an algorithm like backpropagation.

Why is backpropagation needed?

A neural network contains many weights and bias which affect the output of the network when you feed it some input. The whole idea of the neural network model is that

1. you feed some input to the network and get some output;
2. you compare this output with what was the expected output;
3. you tweak the neural network just a tiny bit so that this particular input produces something that is slightly closer to the actual output;
4. you repeat this for various different inputs, in the hopes that these small improvements compound into really good improvements after a lot of iterations.

The backpropagation algorithm is an algorithm you can use to make these small improvements in an efficient way.

Setup

Let us start by defining exactly what we are working with, so that there are no mix-ups.

We will be working with an instance of a NeuralNetwork, that we will refer to as net, that we assume has n layers. That is, n = len(net._layers). Each layer i has a weights matrix, net._layers[i]._W, and a column vector net._layers[i]._b with the biases. Each layer also has an activation function, net._layers[i].act_function.

It is very important to notice that in the code above and throughout this article I will assume the vectors are column vectors.

We have seen that our net has a forward_pass method that depends on the forward_pass of each layer. If we were to write out explicitly the expression for each layer's forward pass, then we would have something like

class NeuralNetwork:
    # ...

    def forward_pass(self, x):
        out = x
        for layer in self._layers:
            out = layer.act_function.f(np.dot(layer._W, out) + layer._b)
        return out

How we set this forward pass up is highly relevant because it will greatly impact the specific details of the algorithm.

Propagation of effects

After the forward pass is complete we will want to see by how much the network got the answer wrong. We do this by measuring the loss with net._loss_function.loss. Then, for each layer, we will want to update layer._W and layer._b so that, next time, the loss is slightly lower (i.e., the answer is slightly more correct).

How do the parameters of the network influence the loss? To answer this, let us first rewrite out network's forward pass slightly, so that we actually save the intermediate values:

class NeuralNetwork:
    # ...

    def forward_pass(self, x):
        xs = [x]
        for layer in self._layers:
            xs.append(layer.forward_pass(xs[-1]))
        return xs

The input to the network is xs[0], and the layer in self._layers[0] will take it and create xs[1].

Then, the layer in self._layers[1] will take it and create xs[2].

Then, the layer in self._layers[2] will take it and create xs[3]...

Up until the point where the layer in self._layers[n-1] takes xs[n-1] and creates xs[n], the final network output. Then, that output xs[n] directly influences the loss, because the loss is net._loss_function.loss(xs[n], t), where t is the target output.

The lines above should paint a picture of "closeness" to the loss, helping you understand that the effects of xs[n] on the loss are much more immediate than the effects of xs[3] on the loss, which in turn are more immediate than the effects of xs[0].

This is why it is so much easier to update the network by starting with the last layer and working your way up to the first layer of the network: because in order to know how a layer influences the loss, you first need to know how the following layer influences the loss.

Matrix calculus

One thing that is noteworthy is that everything becomes much easier if we write the algorithm in terms of operations with matrices, instead of only being allowed to write sums and products of real numbers.

For that matter, we will write everything in terms of matrices and vectors. If you, or someone else, want to know the specific equation for a specific weight, you just have to inspect the appropriate coordinate of the appropriate matrix.

The algorithm

So now that we know that we really need to work our way backwards, we just need to find out a couple more things before we can really implement the method. The two other things we need to know are:

• the derivative of the loss function;
• the derivative of each activation function.

Strictly speaking, we don't really need to know what they are, we just need a way to compute them, and we did that in the previous article in the series. So we have the derivative of the loss function, with respect to the network's output, as net._loss_function.dloss. Similarly, for each layer, we have layer.act_function.df that represents that activation function's derivative.

The backpropagation algorithm is a really clever algorithm because it introduces some intermediate variables that allow us to reuse many computations, speeding up what could be a really slow algorithm.

In order to derive the actual algorithm, we will try to make more clear the recursive pattern we are dealing with. We will be populating three lists, dxs, dWs, and dbs, where:

• dxs[i] quantifies how much xs[i] influences the loss;
• dWs[i] quantifies how much net._layers[i]._W influences the loss; and
• dbs[i] quantifies how much net._layers[i]._b influences the loss.

For convenience, let us also assume Ws is a list with all the weight matrices, bs is a list with all the bias vectors, fs is a list with all the activation functions, and dfs is a list with their derivatives:

Ws = [layer._W for layer in net._layers]
bs = [layer._b for layer in net._layers]
fs = [layer.act_function.f for layer in net._layers]
dfs = [layer.act_function.df for layer in net._layers]

On top of that, let L be the loss function and dL its derivative, as if we had done

L = net._loss_function.loss
dL = net._loss_function.dloss

These assignments aren't strictly needed, but they will make the remainder of the article lighter to follow.

First step

Recall the formula for the loss, if written with the weights and biases from the last layer:

loss = L(fs[n-1](np.dot(Ws[n-1], xs[n-1]) + bs[n-1]), t)

When we have the loss at hands, this is the most recent computation we did, and so it seems reasonable to start by computing dxs[n-1], dWs[n-1] and dbs[n-1]:

y = np.dot(Ws[n-1], xs[n-1]) + bs[n-1]
dbs[n-1] = dfs[n-1](y) * dL(xs[n], t)
dxs[n-1] = np.dot(Ws[n-1].T, dbs[n-1])
dWs[n-1] = np.dot(dbs[n-1], xs[n-1].T)

where .T transposes a vector or matrix. Strictly speaking, dfs[n-1](y) should return a matrix, and we should then use np.dot to multiply with dL(xs[n], t), but it is simpler to implement the derivatives of the activation functions like we have seen, and so we can get away with plain multiplication.

Next step

Now that we know how to quantify the way xs[n-1], Ws[n-1], and bs[n-1] influence the loss (because we just computed dxs[n-1], dMs[n-1] and dbs[n-1]), it is time to quantify how xs[n-2], Ws[n-2] and bs[n-2] influence the loss.

Here is the formula for the loss again, this time showing the dependence on xs[n-2], Ws[n-2] and bs[n-2]:

loss = L(fs[n-1](
    np.dot(
        Ws[n-1],
        fs[n-2](np.dot(Ws[n-2], xs[n-2]) + bs[n-2])
) + bs[n-1]), t)

You may feel it is reasonable, or maybe you don't, but the fact that the dependences on xs[n-2], Ws[n-2] and bs[n-2] are hidden behind xs[n-1] because xs[n-1] = fs[n-2](dot(Ws[n-2], xs[n-2]) + bs[n-2]), means we can compute xs[n-2], Ws[n-2] and bs[n-2] at the expense of dxs[n-1].

After the maths is carried out, the formulas turn out to be:

y = np.dot(Ws[n-2], xs[n-2]) + bs[n-2]
dbs[n-2] = dfs[n-2](y) * dxs[n-1]
dxs[n-2] = np.dot(Ws[n-2].T, dbs[n-2])
dWs[n-2] = np.dot(dbs[n-2], xs[n-2].T)

The general step

I won't spell out another step for you, so I hope you understood by now that the next iteration will be

y = np.dot(Ws[n-3], xs[n-3]) + bs[n-3]
dbs[n-3] = fs[n-3](y) * dL(xs[n-2], t)
dxs[n-3] = np.dot(Ws[n-3].T, dbs[n-3])
dWs[n-3] = np.dot(dbs[n-3], xs[n-3].T)

all the way until

y = np.dot(Ws[0], xs[0]) + bs[0]
dbs[0] = fs[0](y) * dL(xs[1], t)
dxs[0] = np.dot(Ws[0].T, dbs[0])
dWs[0] = np.dot(dbs[0], xs[0].T)

which can be folded into a generic loop where we build the lists dxs, dWs and dbs from the end up to the start:

dbs, dWs = [], []
dxs = [dL(xs[n], t)]
for x, W, b, f in reversed(list(zip(xs[:-1], Ws, bs, fs))):
    y = np.dot(W, x) + b
    dbs.append(f(y) * dxs[-1])
    dxs.append(np.dot(W.T, dbs[-1]))
    dWs.append(np.dot(dbs[-1], x.T))

This shows how ridiculously simple it can be to implement backpropagation if you have access to matrix multiplication. If you don't, I would recommend you either get access to it or implement it yourself.

And this is how you go about implementing backpropagation! If you know calculus I challenge you to derive the formulas all by yourself. I, for one, have derived them repeatedly over the years, as I keep forgetting how everything works. Hopefully this was the last time I did it! Next time I will be checking this article instead of doing all the work all over again.

Training a network

With the backpropagation algorithm we now get access to the derivatives of the loss with respect to the weight matrices and with respect to the bias vectors. With those derivatives we can train the network: the derivative tells you the direction in which to go if you want to increase the function (in this case, the loss), so if you go just a little bit in the opposite direction, the loss will likely decrease a little bit.

Therefore, what we need to do is take that backpropagation loop and, while we compute the successive derivatives, we should subtract a small multiple from the actual parameters:

class NeuralNetwork:
    # ...

    def train(self, x, t):
        """Train the network on input x and expected output t."""

        xs = self.forward_pass(x)
        dx = self._loss_function.dloss(xs.pop(), t)
        for layer in reversed(self._layers):
            # Compute the derivatives
            x = xs.pop()
            y = np.dot(layer._W, x) + layer._b
            db = layer.act_function.df(y) * dx
            dx = np.dot(layer._W.T, db)
            dW = np.dot(db, x.T)
            # Update parameters.
            layer._W -= 0.001*dW
            layer._b -= 0.001*db

To see this is working, we can create a little demo like before. Let us create a small network whose job is to return a vector with 3 zeroes, no matter what the input is. Then, to see the network actually learns, before and after training we compute its loss over some training samples and print it:

if __name__ == "__main__":
    """Demo of a network as a series of layers."""
    # Silly network whose job is to return a vector of 0s no matter what.
    net = NeuralNetwork([
        Layer(2, 4, LeakyReLU()),
        Layer(4, 4, LeakyReLU()),
        Layer(4, 3, LeakyReLU()),
    ], MSELoss())
    t = np.zeros(shape=(3,1))

    loss = 0
    for _ in range(100):
        x = np.random.normal(size=(2,1))
        loss += net.loss(net.forward_pass(x)[-1], t)
    print(loss)

    for _ in range(10000):
        net.train(np.random.normal(size=(2,1)), t)

    loss = 0
    for _ in range(100):
        x = np.random.normal(size=(2,1))
        loss += net.loss(net.forward_pass(x)[-1], t)
    print(loss)

I ran the file once and I obtained the following:

 > python nn.py
9.853435230767493
0.013773771604489364

We can see that the second time we printed the accumulated loss, it was much, much smaller. This means our algorithm is probably working, now we will just clean it up a little bit. For starters, the 0.001 I multiplied the derivatives with was fairly arbitrary, and is generally a parameter of the network itself – the learning rate. Therefore, we will make this number a network parameter.

Next thing we can do is restore the forward_pass to be the function that simply computes the output, and write our own loop in the train function.

With all this in mind, we could get the following:

class NeuralNetwork:
    """A series of connected, compatible layers."""
    def __init__(self, layers, loss_function, learning_rate):
        self._layers = layers
        self._loss_function = loss_function
        self.lr = learning_rate

        # Check layer compatibility
        for (from_, to_) in zip(self._layers[:-1], self._layers[1:]):
            if from_.outs != to_.ins:
                raise ValueError("Layers should have compatible shapes.")

    # ...

    def train(self, x, t):
        """Train the network on input x and expected output t."""

        # Accumulate intermediate results during forward pass.
        xs = [x]
        for layer in self._layers:
            xs.append(layer.forward_pass(xs[-1]))

        dx = self._loss_function.dloss(xs.pop(), t)
        for layer, x in zip(self._layers[::-1], xs[::-1]):
            # Compute the derivatives
            y = np.dot(layer._W, x) + layer._b
            db = layer.act_function.df(y) * dx
            dx = np.dot(layer._W.T, db)
            dW = np.dot(db, x.T)
            # Update parameters.
            layer._W -= self.lr * dW
            layer._b -= self.lr * db

Now the demo should also be updated, because we just returned the net.forward_pass method to its original state. But now we have reached a point where we can actually use the network for interesting things, so for this demo let us create a separate file.

Distinguishing the quadrant of the points

In a file examples/quadrants.py I wrote the following code:

import sys, pathlib
# (Ugly) workaround to enable importing from parent folder without too much hassle.
sys.path.append(str(pathlib.Path(__file__).parent.parent))

from nn import NeuralNetwork, Layer, LeakyReLU, MSELoss
# import matplotlib.pyplot as plt
import numpy as np

def col(a):
    """Make sure the array is a column."""
    return np.atleast_2d(a).T

N = 100_000     # Create N points inside the square [-2,2]×[-2,2]
data = np.random.uniform(low=-2, high=2, size=(2, N))

ts = np.zeros(shape=(2, N))
ts[0, data[0,]*data[1,]>0] = 1
ts[1, :] = 1 - ts[0, :]

net = NeuralNetwork([
    Layer(2, 3, LeakyReLU()),
    Layer(3, 2, LeakyReLU()),
], MSELoss(), 0.05)

def assess(net, data, ts):
    correct = 0
    # cs = []
    for i in range(data.shape[1]):
        out = net.forward_pass(col(data[:, i]))
        guess = np.argmax(np.ndarray.flatten(out))
        if ts[guess, i]:
            correct += 1
        # cs.append(guess)
    # fig = plt.figure()
    # plt.scatter(data[0, :1000], data[1, :1000], c=cs)
    # fig.show()
    # input()
    return correct

test_to = 1000
print(assess(net, data[:, :test_to], ts[:, :test_to]))
for i in range(test_to, N):
    net.train(col(data[:, i]), col(ts[:, i]))
print(assess(net, data[:, :test_to], ts[:, :test_to]))

What this does is create a series of points inside the square of side length 4 centred in the origin, and then try to distinguish the points in the upper-right and bottom-left corners from the ones in the top-left and lower-right corners.

The lines that are commented out are just a quick and dirty way of visualising the guesses that the network is making. If you have matplotlib available, you can uncomment those and you may get something like the figures below.

The first figure shows the network trying to distinguish the points before training (we can see the network thinks all points are the same), and the next figure shows the network already distinguishes many points.

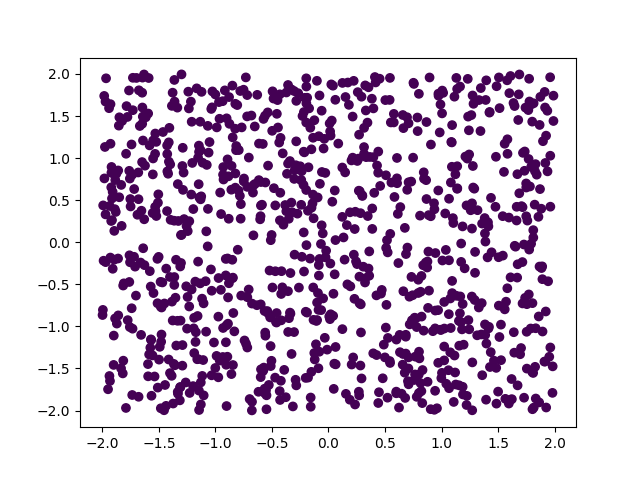
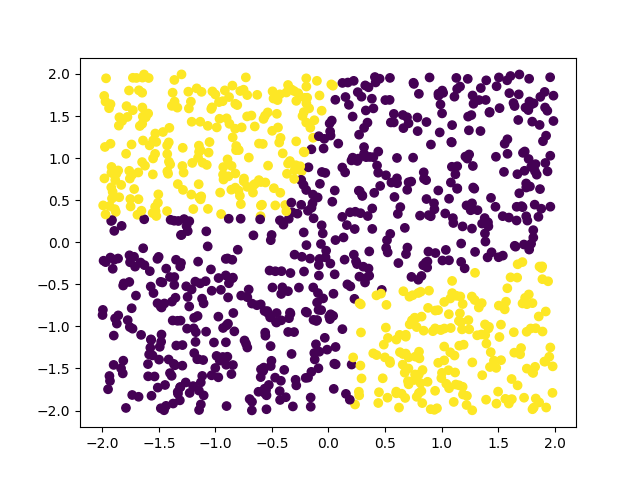
Wrap-up & current code

At this point, the implementation of the network should take up about 110 lines of code of your main file, plus two dozen more for a small demo that shows your network is learning. Notice that, at this point, the neural network implementation is working and ready to be used! Because of that, we can now release v1.0 of our code!

You can find all the code for this series in this GitHub repository and you can find v1.0 (that is, specifically what we built in this article) under the tag v1.0.

In the next article of this short series we will be using our network to recognise handwritten digits in small images! Stay tuned for that.

The series

These are all the articles in this series:

1. Neural networks fundamentals with Python – intro
2. Neural networks fundamentals with Python – network & loss
3. Neural networks fundamentals with Python – backpropagation
4. Neural networks fundamentals with Python – MNIST
5. Neural networks fundamentals with Python – subtleties
6. Neural networks fundamentals with Python – student-teacher

Become a better Python 🐍 developer 🚀

+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!

My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.