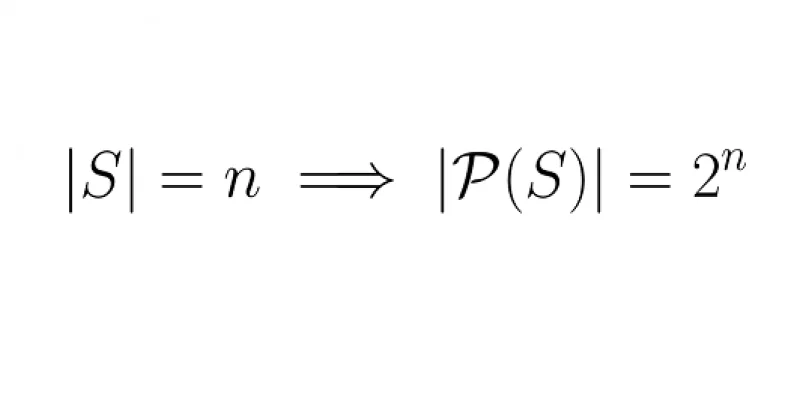This article shows how to do base conversions in Python with the built-in int, how to write integer literals in other bases, and how to do base conversions in general.
Please help me identify these 100 light bulbs by turning ON and OFF their switches.
Today I learned about the symmetry in indexing from the beginning and end of a list with the bitwise invert operator.
This problem is a step up from Problem #028 - hidden key. Can you tackle this one?
There is a key hidden in one of three boxes and each box has a coin on top of it. Can you use the coins to let your friend know where the key is hiding?
Some people are standing quiet in a line, each person with a hat that has one of two colours. How many people can guess their colour correctly?
Let's prove that, if a set has size \(n\), then that same set has exactly \(2^n\) subsets.
This post gives you the code to mess around with "Tupper's self-referential formula", a formula that plots itself.
This problem is a really interesting problem I solved two times. The first time I solved it I failed to prove exactly how it works... then some years later I remembered the problem statement and was able to solve it properly. Let's see how you do!