At operator @
Since Python 3.5, Python has the infix operator @.
This operator was introduced with PEP 465 to be used in matrix multiplication.
You can try to use it with just vanilla Python,
but no vanilla Python types define their behaviour with @:
>>> 3 @ 5
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for @: 'int' and 'int'However, just looking at the error above, you see that the error is in @
not knowing what to do with integers.
The error is not the fact that @ is an invalid operator!
So cool!
Matrix multiplication in numpy with @
If you have numpy at hand, you can check @ works,
because numpy arrays added support to be used with @:
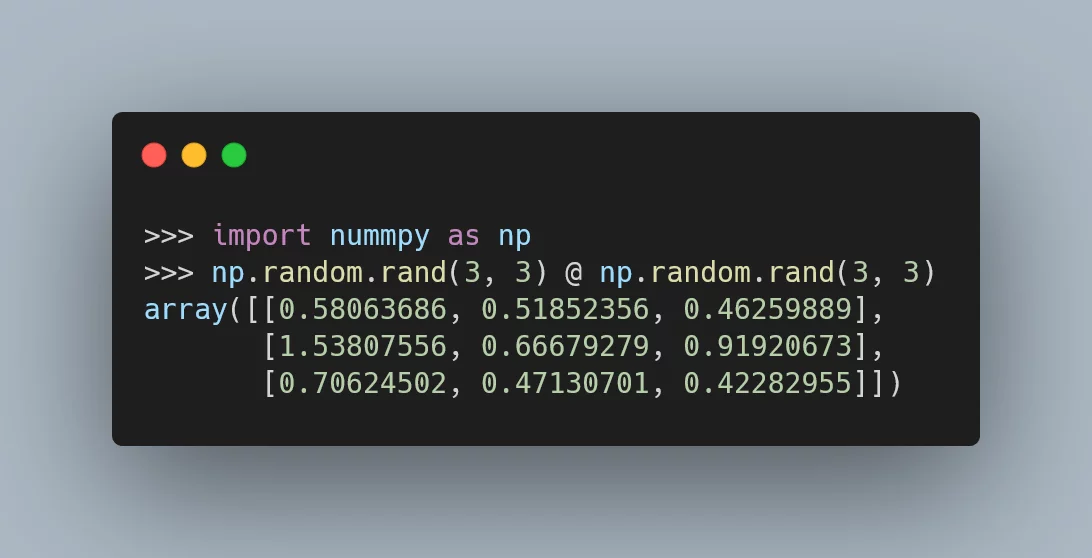
>>> import numpy as np
>>> np.random.rand(3, 3) @ np.random.rand(3, 3)
array([[0.89431673, 0.57949659, 0.59470797],
[0.47364302, 0.29837518, 0.33552972],
[1.12634752, 0.75218169, 0.78876082]])
>>> _ @ np.eye(3) # The identity (eye) matrix leaves the other matrix unchanged.
array([[0.89431673, 0.57949659, 0.59470797],
[0.47364302, 0.29837518, 0.33552972],
[1.12634752, 0.75218169, 0.78876082]])_ is just a way to refer to the last result of the REPL.
Read about it in this Pydon't.
Using @ with custom classes/types
If you want your own objects to add support for @,
all you have to do is implement the dunder methods __matmul__ and __rmatmul__:
>>> class Dummy:
... def __matmul__(self, other):
... print("Works!")
... return 42
... def __rmatmul__(self, other):
... print("Also works!")
... return 73
...
>>> d = Dummy()
>>> d @ 1
Works!
42
>>> 1 @ d
Also works!
73There's also the __imatmul__ method for in-place matrix multiplication:
>>> class Dummy:
... def __imatmul__(self, other):
... print("In-place!")
...
>>> d = Dummy()
>>> d @= 1
In-place!Of course, this silly example above doesn't show you the proper semantics of the __matmul__,
__rmatmul__, and __imatmul__ methods.
It just shows you they exist and they interact with the operator @!
By the way, for reference, here is the tweet that showed me this:
How did I not know @ was a proper operator?!
— Rodrigo 🐍📝 (@mathsppblog) October 12, 2021
That's it for now! Stay tuned and I'll see you around!
Become the smartest Python 🐍 developer in the room 🚀
Every Monday, you'll get a Python deep dive that unpacks a topic with analogies, diagrams, and code examples so you can write clearer, faster, and more idiomatic code.
