Reverse-engineering the program from “Chronospatial Computer”, day 17 of Advent of Code 2024.
Solving “Bridge Repair”, from day 7 of Advent of Code 2024, in 4ms with Python with a simple deductive algorithm.
Can you solve this crossword where all hints are regular expressions?
With a couple of loops and a bit of maths you can create a rotating spiral.
This article shows how to do base conversions in Python with the built-in int, how to write integer literals in other bases, and how to do base conversions in general.
The built-in function max in Python is broken and this article explains why, drawing parallels with other programming and mathematics concepts.
How can an infinite number of mathematicians figure out their own hat colours?
This article shows how to use the Python built-in divmod for unit conversions.
Today I learned that Python and other programming languages have negative zero, -0.0.
Create a zooming animation from first principles in Python. In 5 minutes. Kind of.
Create animations from first principles and morph between different figures with Python. In 5 minutes. Kind of.
Today I learned how to draw a Bézier curve with the De Casteljau's algorithm.
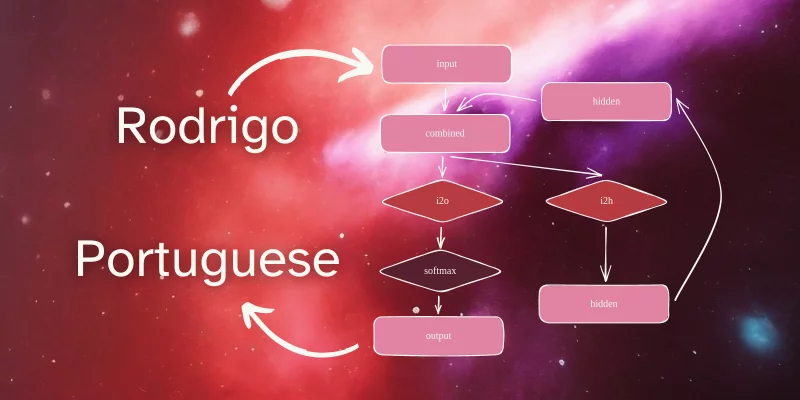
In this introductory tutorial, you will build a recurrent neural network (RNN) with PyTorch.
Go through the complete code for a Python project that consists in finding similar photographs in a folder. This tutorial will make use of classical techniques and is suitable for beginners.
Can you prove that there are arbitrarily many primes in arbitrarily big intervals?
Today I (re)learned Heron's formula to compute the area of a triangle from its three sides.
