Alice and Bob sit across each other, ready for their game of coins. Who will emerge victorious?
This is an algorithmic puzzle where you just have to turn some coins.
In the fifth article of this short series we will be handling some subtleties that we overlooked in our experiment to classify handwritten digits from the MNIST dataset.
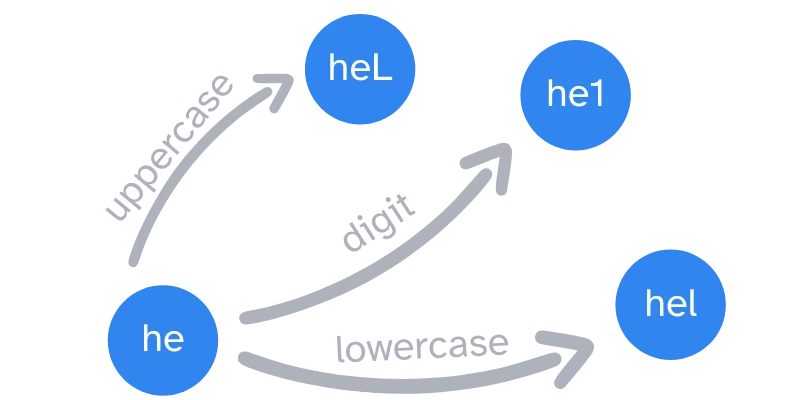
In this article we use (finite state) automatons to count 698,438,863,898,480,640 passwords in a couple milliseconds.
Two doors, one gives you eternal happiness and the other eternal sadness. How can you pick the correct one?
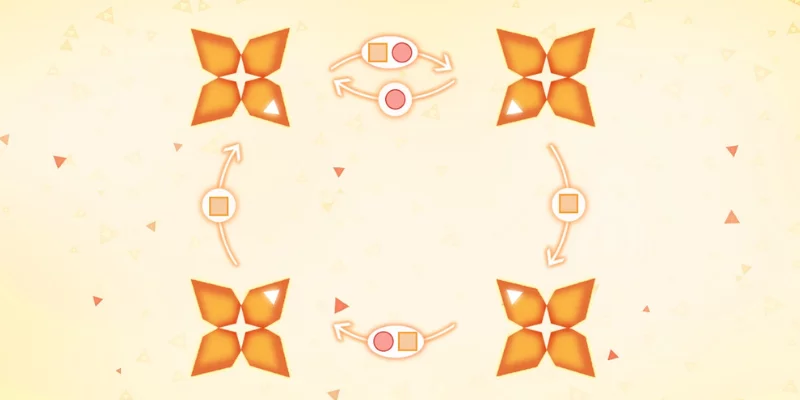
Syncro is a beautiful game where you have to unite all the petals in a single flower. In how many moves can you do it?
A waiter at a restaurant gets a group's order completely wrong. Can you turn the table to get two or more orders right?
In the fourth article of this short series we will apply our neural network framework to recognise handwritten digits.
A bunch of ants are left inside a very, very, tight tube, and they keep colliding with each other and turning around. How long will it take them to escape?
The third article of this short series concerns itself with the implementation of the backpropagation algorithm, the usual choice of algorithm used to enable a neural network to learn.
In the second article of this short series we will create a class for a generic neural network and we will also see how to assess the quality of the output of a network, essentially preparing ourselves to implement the backpropagation algorithm.
This is the first article in a series to implement a neural network from scratch. We will set things up in terms of software to install, knowledge we need, and some code to serve as backbone for the remainder of the series.
You are sunbathing when you decide to go and talk to some friends under a nearby sun umbrella, but first you want to get your feet wet in the water. What is the most efficient way to do this?
This problem is a step up from Problem #028 - hidden key. Can you tackle this one?
Nowadays stores come up with all sorts of funky promotions to catch your eye... But how much money do you actually save with each type of promotion?
There is a key hidden in one of three boxes and each box has a coin on top of it. Can you use the coins to let your friend know where the key is hiding?
Five sailors and their monkey were washed ashore on a desert island. They decide to go get coconuts that they pile up. During the night, each of the sailors, suspicious the others wouldn't behave fairly, went to the pile of coconuts take their fair share. How many coconuts were there in the beginning..?
I bet you have seen one of those Facebook publications where you have a grid and you have to count the number of squares the grid contains, and then you jump to the comment section and virtually no one agrees on what the correct answer should be... Let's settle this once and for all!
Some people are standing quiet in a line, each person with a hat that has one of two colours. How many people can guess their colour correctly?
