Today I learned how to quickly switch back and forth between two different git branches.
Today I learned how to publish a Python package to PyPI with uv.
This is a short account of how I wrote a program that solves all LQueens puzzles from LinkedIn automatically with Python.
The 10th article of this series adds support for elif and else statements.
This practical tutorial shows how to use uv to build and install custom Python CLI applications globally on your system.
You can ignore exceptions with contextlib.suppress and in this article I show why this is preferred over try: ... except: pass.
Today I learned that I can use the percent sign to run commands from inside Jupyter notebooks.
Today I learned that Python has nested Easter eggs in the standard library.
Today I learned that Polars allows non-strict vertical concatenation of dataframes with the parameter how="vertical".
Today I learned how to create standalone Python scripts with uv.
I used an LLM to write a countdown timer and I have mixed feelings about the result.
Today I learned how I can use the method 'groupdict' from a regex match to get a dictionary with all named groups.
In this article I explore functools.cmp_to_key and propose a possible implementation.
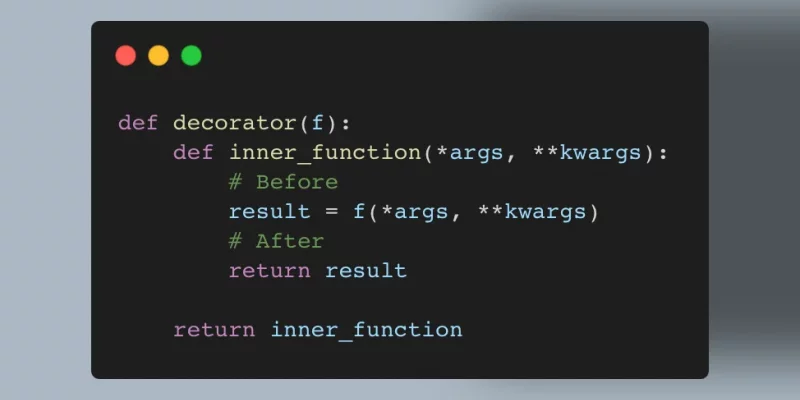
This article teaches the decorator pattern in Python, why it exists, how to use it, and when to use it to write efficient and idiomatic Python code.
Today I learned that if you suppress the exception KeyboardInterrupt then your program is still interrupted but it doesn't display a traceback.
Today I learned that the hash of an integer is the integer itself, except for -1. The hash of -1 is -2.
Today I learned how to allow my custom objects to be unpacked into keyword arguments like '**kwargs'.
Reverse-engineering the program from “Chronospatial Computer”, day 17 of Advent of Code 2024.