This tutorial will introduce beginners to the many features that Textual offers to build elegant and lightweight TUIs.
Today I learned how to create nested git repositories through the submodules command.
Today I learned how to create a VS Code extension to do custom syntax highlighting.
Today I learned how to create an alias to activate my Python virtual environments with a single-word command.
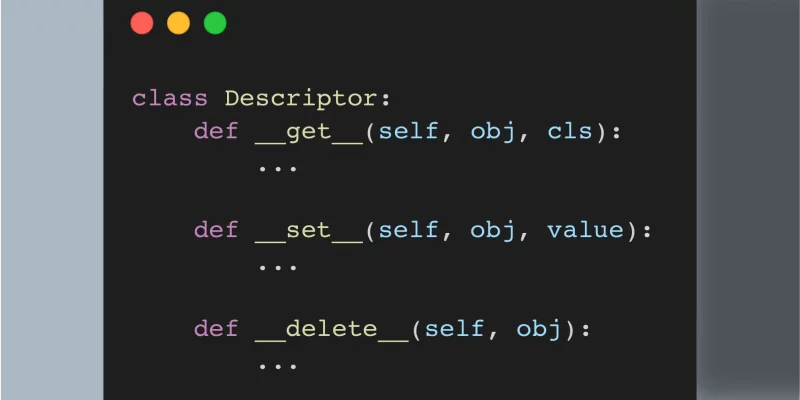
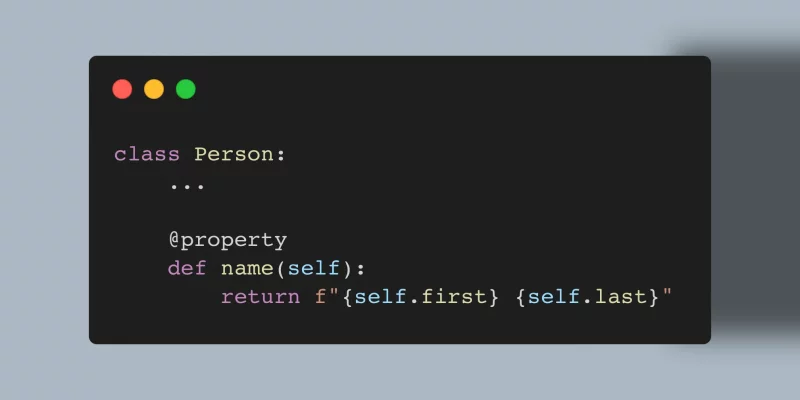
Descriptors are not black magic and this article will show you that. In fact, you use descriptors every day and you don't even know it.
Today I learned how to skip tests on Microsoft Windows in pytest.
This is a short tutorial on how to use modal screens with Textual.
Today I learned why I should use the dbg! macro instead of the println! macro for debugging in Rust.
Today I learned how to use the VS Code debugger in code from “other” modules.
Today I learned how to optimise my website images for the web and I automated that process.
This reference article teaches you the things you'll need to write your thesis or report with LaTeX.
This short reference article shows how to stream data from a Flask web app to HTMX using server-side events (SSE).