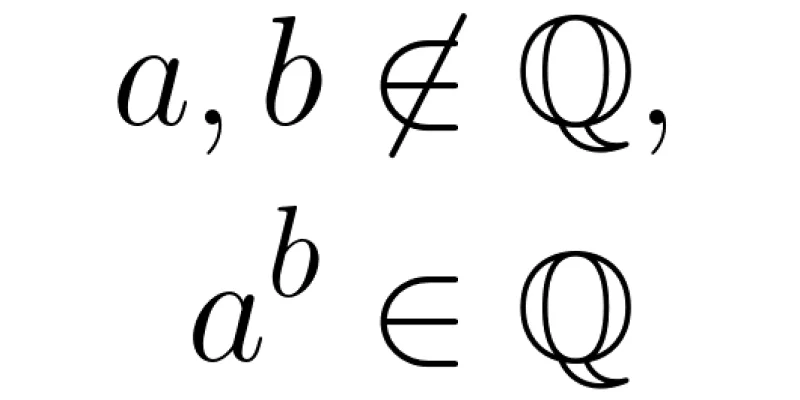Given some paper squares, can you slice them and then glue them back together to form a single square?
Is it true that every integer you can think of has a multiple written out only with \(0\)s and \(1\)s?
I find the problem in this post rather fun to think about because it is a problem about a game that can actually be played between two players.
In this post we will talk about three different, all very common, ways of writing proofs: proofs by construction, by contrapositive and by contradiction.
This problem is a really interesting problem I solved two times. The first time I solved it I failed to prove exactly how it works... then some years later I remembered the problem statement and was able to solve it properly. Let's see how you do!
In this post I talked about the riddle of the water buckets. Now I challenge you to prove that in some situations it is impossible to solve it!
Can you measure exactly \(2\)L of water with two plain buckets with volumes of \(14\)L and \(5\)L? Of course you can!
Let's prove that there are two irrational numbers, call them \(a\) and \(b\), such that \(a^b\) is a rational number! And let's do it in a tweet.
Gandalf has some Hobbits to appease but his task seems to go on forever. Can you give him a hand..?
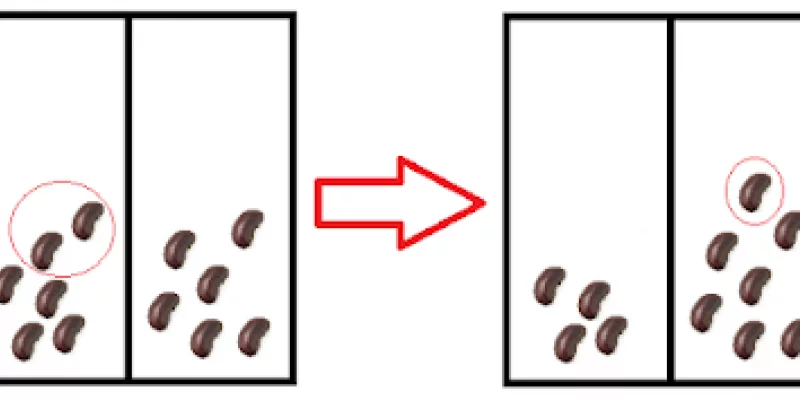
Two friends were bored and decided to play a game... a mathematical game with a paper bag!
This post's format will be a bit different from the usual and the first of a series of posts of this type. In this post, I will state a problem and then present my solution.
Here's how I like to solve my equations: just walk around randomly until I trip over a solution!
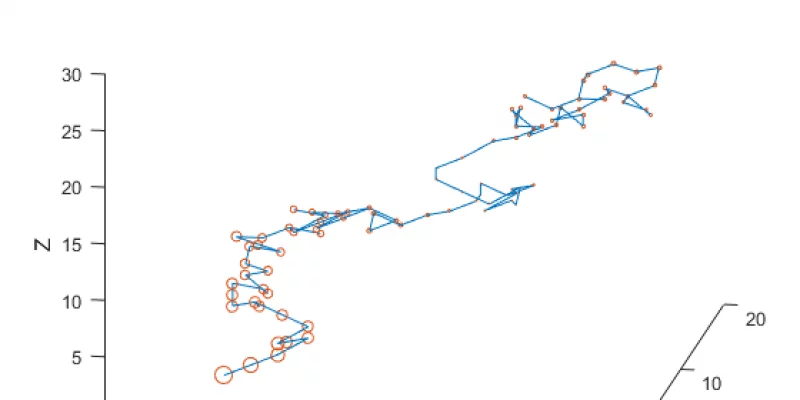
Think of a drunk man that continuously tumbles left and right, back and forth, with no final destination.
Progress is great and new things are always exciting... but that doesn't mean old things don't have any value!
The filled Julia set is a really cool fractal that kind of resembles the Mandelbrot set!
In this post I just ramble a bit through some mathematician's definition of what a recursive function is...
I have always liked the concept of fractal. They are very beautiful, they have a notion of infinity embedded in them, and they make no sense (seriously though, self-similarity?). How could they not be loved?
