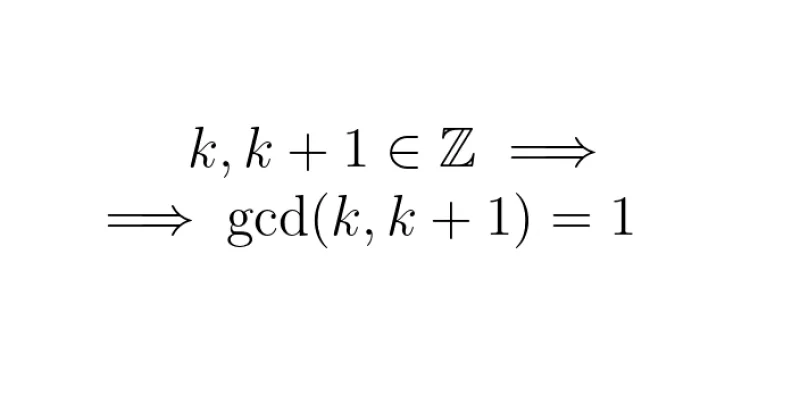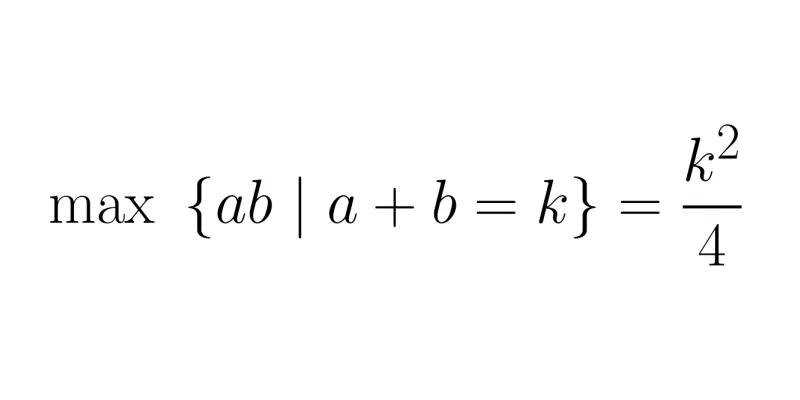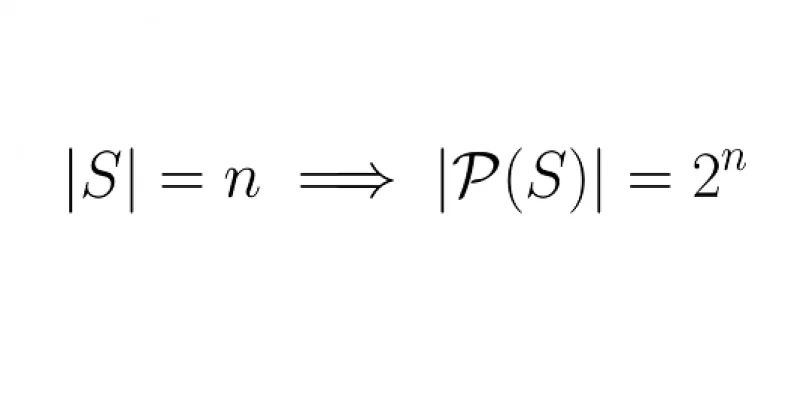Join me in this blog post for Pokéfans and mathematicians alike. Together we'll find out how long it would take to fill your complete Pokédex by only performing random trades.
In this problem you have to devise a strategy to beat the computer in a "guess the polynomial" game.
Let's prove that if \(k\) is an integer, then \(\gcd(k, k+1) = 1\). That is, any two consecutive integers are coprime.
Let's prove that if you want to maximise \(ab\) with \(a + b\) equal to a constant value \(k\), then you want \(a = b = \frac{k}{2}\).
This simple problem is an example of a very interesting phenomenon: if you have a large enough "universe" to consider, even randomly picked parts exhibit structured properties.
Let's prove that, if a set has size \(n\), then that same set has exactly \(2^n\) subsets.
The 24 Game is a well-known maths game that is played with kids in school to help them master the four basic arithmetic operations. In this blog post we will study the game in depth.
Today we are visiting a specific instance of a well-known basic mathematics game, the 24 Game. The "24 Game" is usually played with younger students because it helps them develop skills related to the basic arithmetic operations.
Take out a piece of paper and a pencil, I am going to ask you to write some letters in your sheet of paper and then I am going to challenge you to fold the sheet of paper... with a twist!
\(n\) mathematicians with numbered party hats gather around in a circle... It is a matter of life or death!
There's 100 drawers and 100 shuffled balls. Can you find the one I choose?
Can you cover all of the rational numbers in [0, 1] with tiny intervals?
Split the numbers 0, 1, ..., 15 into two sets with sum interesting properties!
In high school I had a colleague that had his birthday on the same day as I did. What a coincidence, right? Right..?
