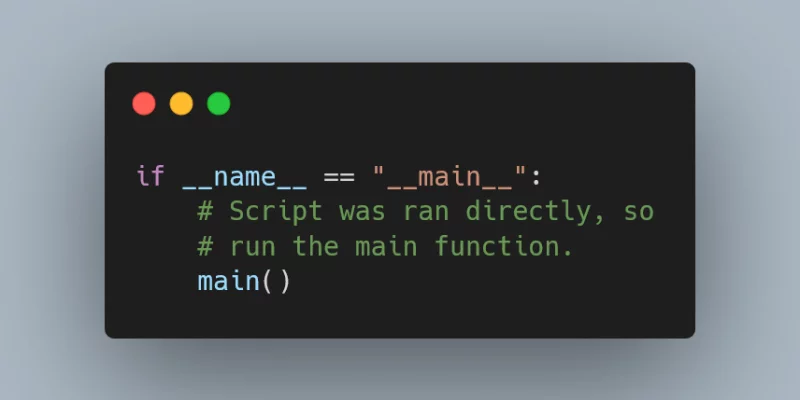
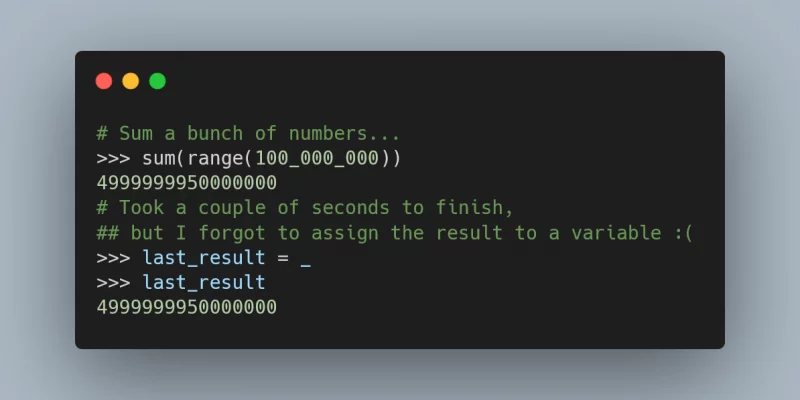
This Pydon't walks you through the usages of the
__name__ dunder method and how to use it effectively.
You have two magical ropes that you can set on fire and you need to count 45 minutes. How do you do it?
The purpose of this Pydon't is to show you what underscores are used for in Python, and to show you how to write more idiomatic code with them.
You are on vacation and must find the most efficient way to cross all bridges. How will you do that?
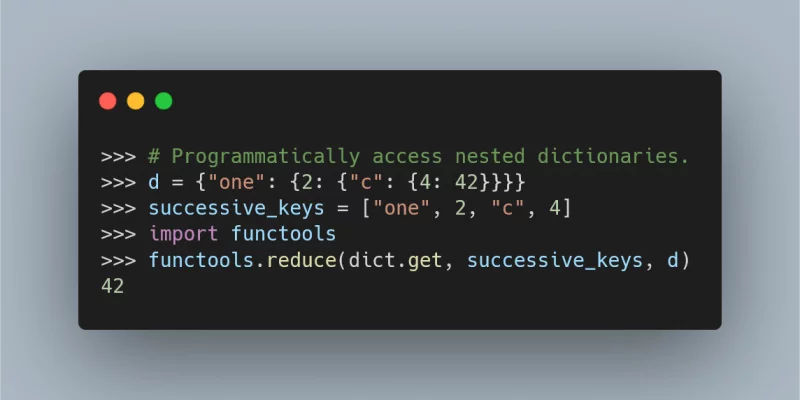
In this Pydon't we will take a look at the reduce function,
which used to be a built-in function and is currently
in the functools module.
This article will twist and bend your mind a little bit, as we go over some interesting self-referential concepts and objects.
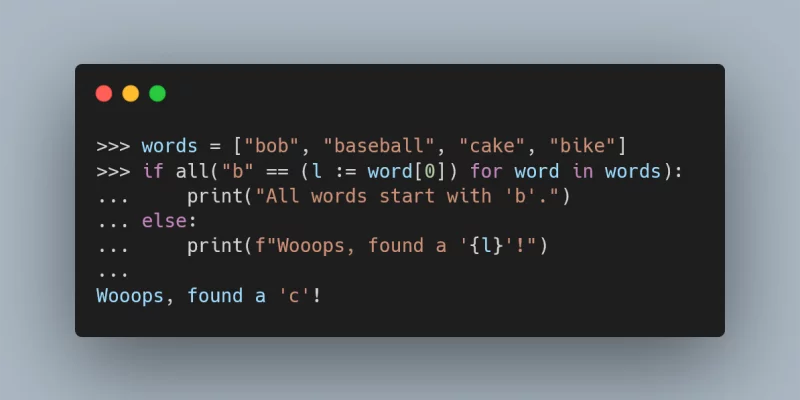
In this Pydon't we explore what Boolean short-circuiting
for the and and or operators is, and how to use this
functionality to write more expressive code.
Alice and Bob sit across each other, ready for their game of coins. Who will emerge victorious?
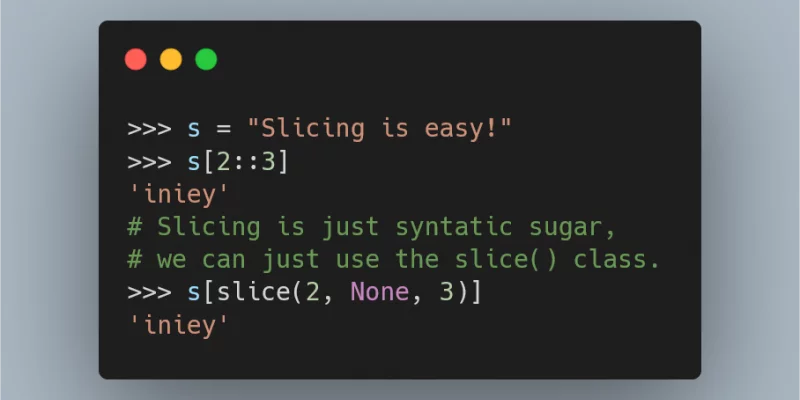
In this Pydon't we conclude the slicing trilogy and
take a look at the inner workings of Python slicing,
from the built-in slice type to the dunder method
__getitem__ and its siblings.
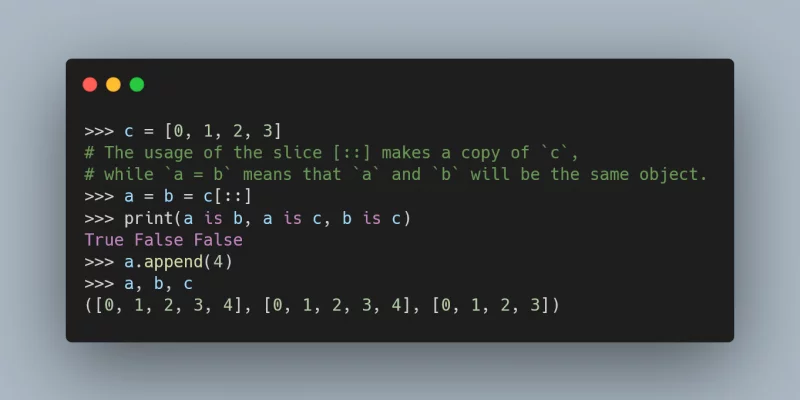
In this Pydon't we cover advanced topics related to sequence slicing, like (negative) steps, more idiomatic sequence slicing, slice assignment, and slice deletion.
This is an algorithmic puzzle where you just have to turn some coins.
In the fifth article of this short series we will be handling some subtleties that we overlooked in our experiment to classify handwritten digits from the MNIST dataset.
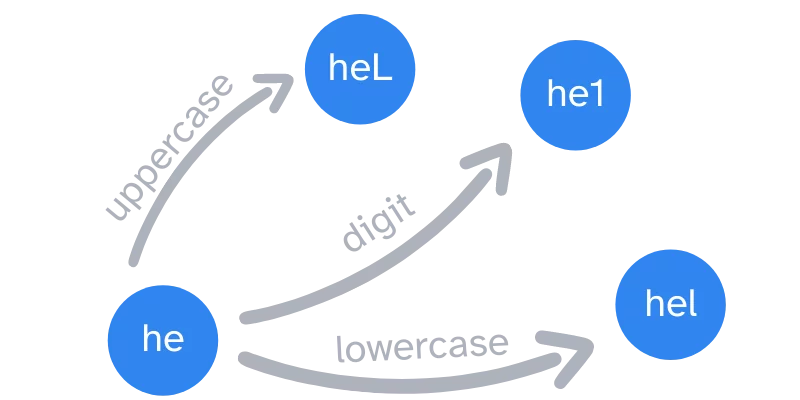
This article covers the basics of sequence slicing in Python and teaches you some idiomatic slicing patterns to write more elegant code.
In this article we use (finite state) automatons to count 698,438,863,898,480,640 passwords in a couple milliseconds.
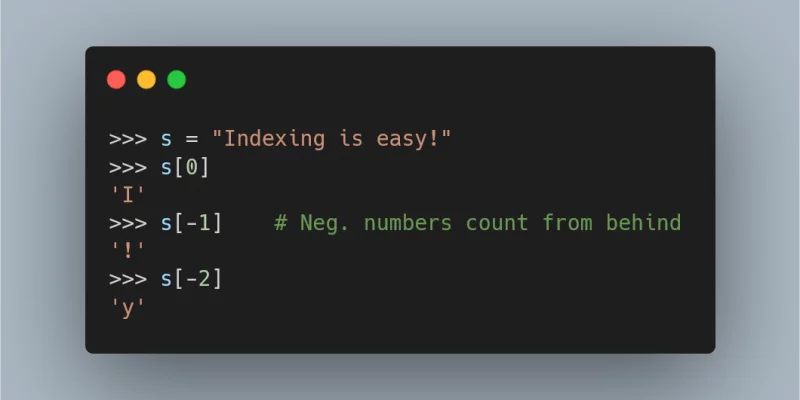
A short article with all you need to know about sequence indexing in Python – and a bit more.
Two doors, one gives you eternal happiness and the other eternal sadness. How can you pick the correct one?
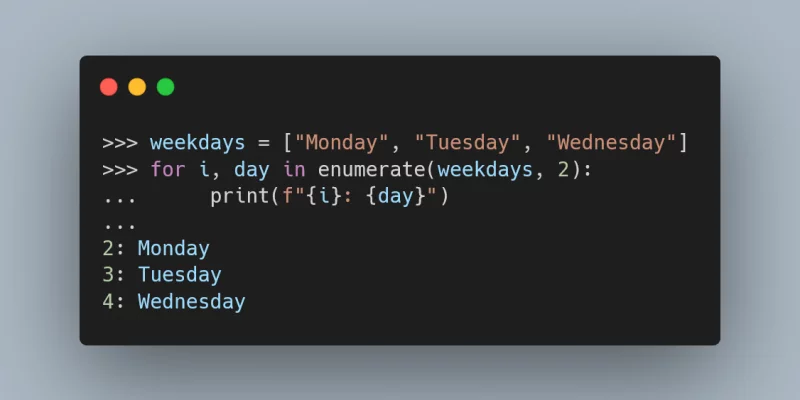
If you need to access the items of an iterable but also keep
track of their indices, have you considered using enumerate?
Let's talk about another of Python's amazing tools to work
with for loops.
Syncro is a beautiful game where you have to unite all the petals in a single flower. In how many moves can you do it?