In part 4 of this series we add some unit testing,
improve our tokenizer and implement the primitives ⍴ and ⍤.
for loops are the bread and butter of imperative programming
and Python has some really nice tools to work with them.
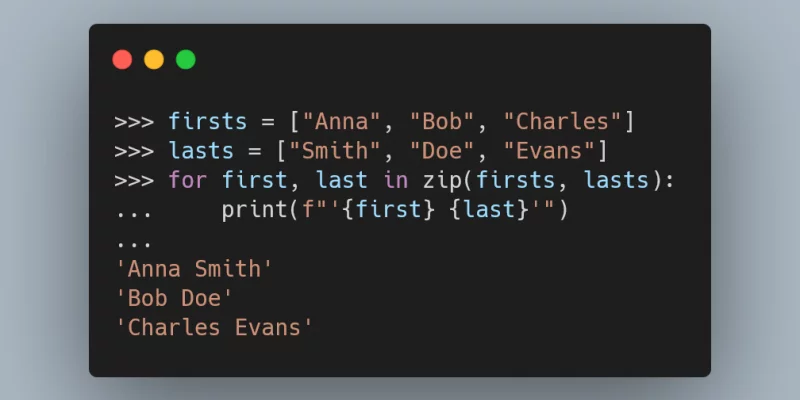
If you want to traverse several structures in parallel,
have you considered using zip?
A waiter at a restaurant gets a group's order completely wrong. Can you turn the table to get two or more orders right?
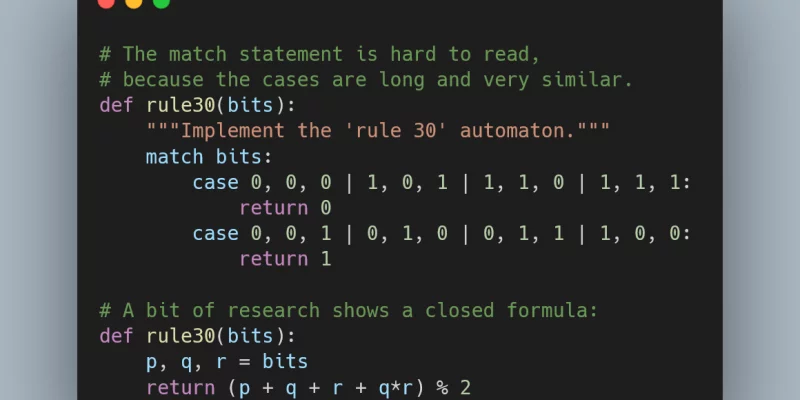
Structural pattern matching is coming in Python 3.10 and
the previous Pydon't explored some interesting use cases
for the new match statement.
This article explores situations for which match isn't the answer.
In the fourth article of this short series we will apply our neural network framework to recognise handwritten digits.
Structural pattern matching is coming in Python 3.10 and this article
explores how to use it to write Pythonic code,
showing the best use cases for the match statement.
A bunch of ants are left inside a very, very, tight tube, and they keep colliding with each other and turning around. How long will it take them to escape?
The third article of this short series concerns itself with the implementation of the backpropagation algorithm, the usual choice of algorithm used to enable a neural network to learn.
In the second article of this short series we will create a class for a generic neural network and we will also see how to assess the quality of the output of a network, essentially preparing ourselves to implement the backpropagation algorithm.
This is the first article in a series to implement a neural network from scratch. We will set things up in terms of software to install, knowledge we need, and some code to serve as backbone for the remainder of the series.
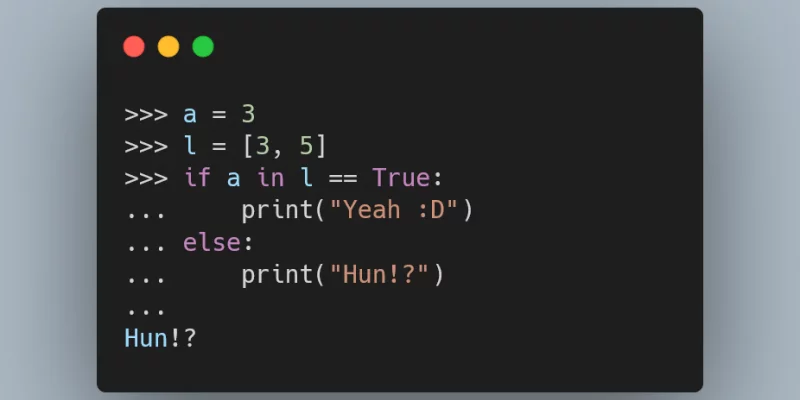
Learn the ins and outs of comparison operator chaining, and especially the cases you should avoid.
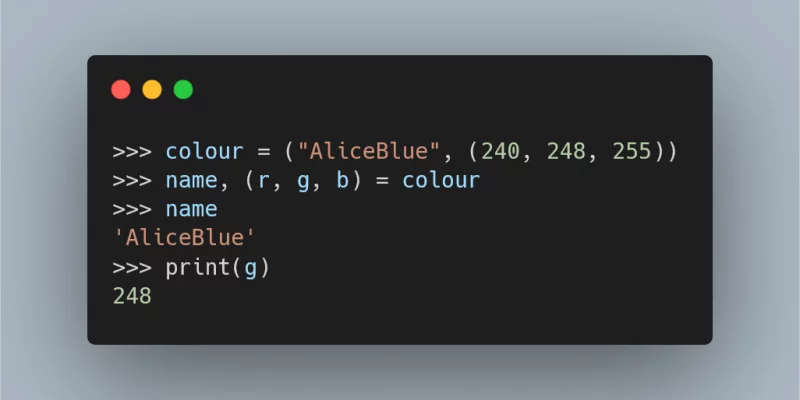
Learn about deep unpacking, a powerful way to write assignments in your code that protects you against unexpected bugs and that you'll rely on heavily when using the structural pattern matching feature that was introduced in Python 3.10.
You are sunbathing when you decide to go and talk to some friends under a nearby sun umbrella, but first you want to get your feet wet in the water. What is the most efficient way to do this?
Recursion is a technique that you should have in your programming arsenal, but that doesn't mean you should always use recursion when writing Python code. Sometimes you should convert the recursion to another programming style or come up with a different algorithm altogether.
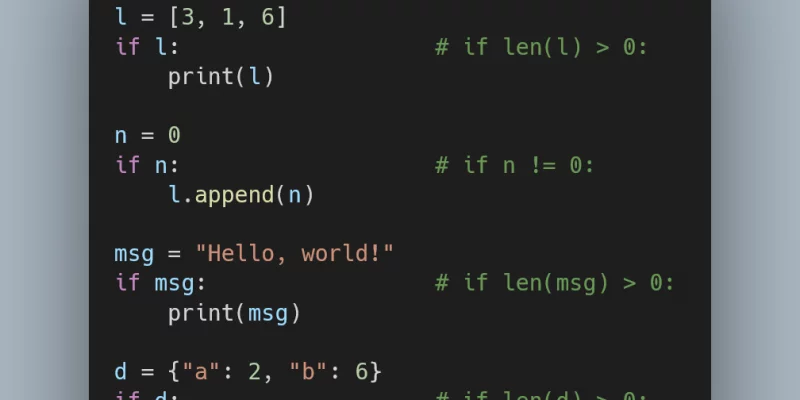
All Python objects can be used in expressions that should
return a boolean value, like in an if or while statement.
Python's built-in objects are usually Falsy (interpreted as False)
when they are “empty” or have “no value” and otherwise they
are Truthy (interpreted as True).
You can define this behaviour explicitly for your own
objects if you define the __bool__ dunder method.
This problem is a step up from Problem #028 - hidden key. Can you tackle this one?
Python's str and repr built-in methods are similar, but not the same.
Use str to print nice-looking strings for end users and use repr for debugging
purposes.
Similarly, in your classes you should implement the __str__ and __repr__
dunder methods with these two use cases in mind.
Nowadays stores come up with all sorts of funky promotions to catch your eye... But how much money do you actually save with each type of promotion?
The walrus operator := can be really helpful, but if you use it in convoluted
ways it will make your code worse instead of better.
Use := to flatten a sequence of nested ifs or to reuse partial computations.
There is a key hidden in one of three boxes and each box has a coin on top of it. Can you use the coins to let your friend know where the key is hiding?