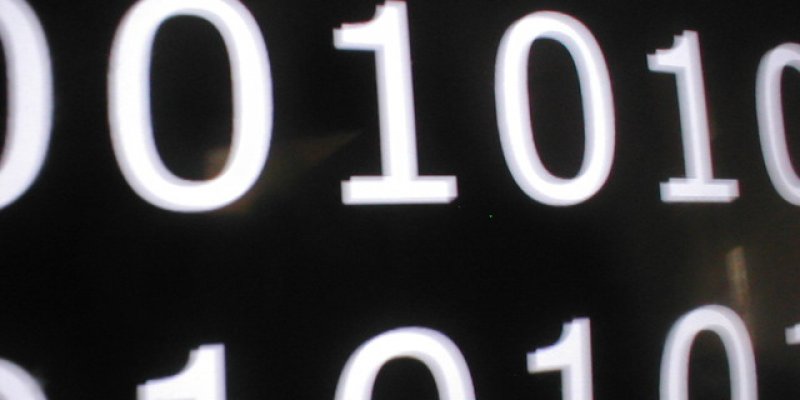I bet you have seen one of those Facebook publications where you have a grid and you have to count the number of squares the grid contains, and then you jump to the comment section and virtually no one agrees on what the correct answer should be... Let's settle this once and for all!
Alice and Bob sit down, face to face, with a chessboard in front of them. They are going to play a little game, but this game only has a single knight... Who will win?
Some people are standing quiet in a line, each person with a hat that has one of two colours. How many people can guess their colour correctly?
In this problem you have to devise a strategy to beat the computer in a "guess the polynomial" game.
This simple problem is an example of a very interesting phenomenon: if you have a large enough "universe" to consider, even randomly picked parts exhibit structured properties.
Alice and Bob are going to be locked away separately and their faith depends on their guessing random coin tosses!
Today we are visiting a specific instance of a well-known basic mathematics game, the 24 Game. The "24 Game" is usually played with younger students because it helps them develop skills related to the basic arithmetic operations.
Take out a piece of paper and a pencil, I am going to ask you to write some letters in your sheet of paper and then I am going to challenge you to fold the sheet of paper... with a twist!
\(n\) mathematicians with numbered party hats gather around in a circle... It is a matter of life or death!
There's 100 drawers and 100 shuffled balls. Can you find the one I choose?
Can you cover all of the rational numbers in [0, 1] with tiny intervals?
Split the numbers 0, 1, ..., 15 into two sets with sum interesting properties!
Given some paper squares, can you slice them and then glue them back together to form a single square?
Is it true that every integer you can think of has a multiple written out only with \(0\)s and \(1\)s?