This problem is a step up from Problem #028 - hidden key. Can you tackle this one?

Problem statement
You and your best friend are locked in jail for no reason at all, but you are given the opportunity to escape. You are taken to a room that has four opaque boxes. The key to your cell will be put inside one of the boxes, and then a (regular) coin is placed on top of each box. You may pick a single coin and reverse its face up, and then your friend will enter the room.
When your friend enters the room you are not allowed to talk, and your friend must open a box. If your friend opens the box with the key, you are set free. Otherwise, you are locked for eternity...
What is the strategy that you and your friend should agree upon, so that your friend can always find the key?
Give it some thought...
If you need any clarification whatsoever, feel free to ask in the comment section below.
Solution
The solution I will be sharing is not the original solution I thought of, I decided to share with you the solution that someone [posted][reddit-sol] online when I shared this puzzle on reddit.
What we are going to do is imagine the four boxes are laid out in a two by two square:

The next thing we do is interpret the sides of the coins as zeroes and ones, because it is easier to do maths with binary numbers. So a random configuration of the coins (of the zeroes and ones) and the (hidden) key could be:
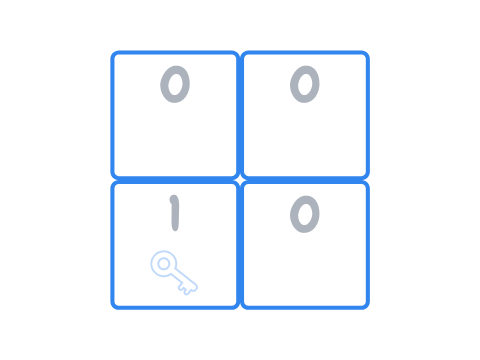
The next thing we do is agree that each box can be represented by its coordinates, in the sense that we can identify each box by the row and column it is in. To make things easier for us, we will start counting the rows and columns from zero, so that the top left box is in position \((0, 0)\), the top right box is in position \((0, 1)\), the bottom left box is in position \((1, 0)\) and the bottom right box is in position \((1, 1)\):
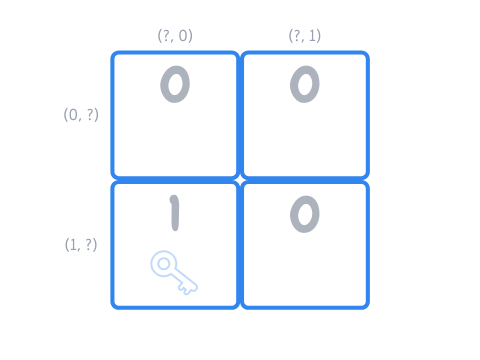
In the example image above, the key is currently in box \((1, 0)\).
Now that we have settled all the important details, we can determine our strategy:
- the parity of the sum of the first row of zeroes and ones will encode the row the key is in; and
- the parity of the sum of the first column of zeroes and ones will encode the column the key is in.
We are talking about the “parity” of the sum because if the row contains two \(1\)s, then we sum them and get \(2\), which is not a valid row. Likewise for the columns. Hence, if the first row sums to an even number, then the key is in the first row, and if the first row sums to an odd number, then the key is in the second row. Similarly, if the first column sums to an even number, then the key is in the first column, and if the first column sums to an odd number, then the key is in the second column.
In our example, the first row sums to \(0\) and the first column sums to \(1\), which indicates that the key should be in box \((0, 1)\), which is wrong:
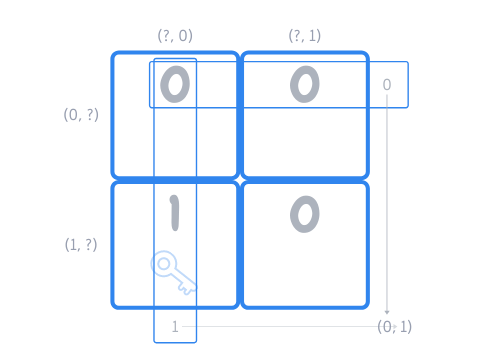
To solve our example, what we would have to do is flip the top left coin (i.e., make it a \(1\)) so that both the first row and the first column now got the correct sum:
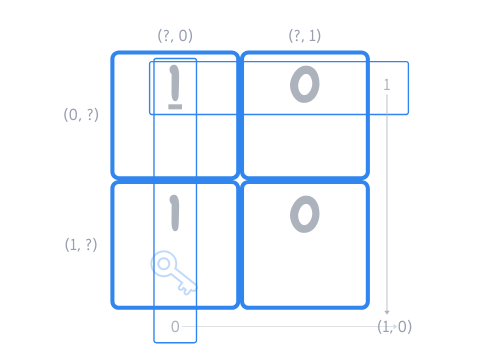
We can see that this strategy always works:
- if the \(0\)s and \(1\)s are already correct, we can flip the coin of the bottom right box;
- if the \(0\)s and \(1\)s already tell us the correct row, but the incorrect column, flip the coin of the bottom left box;
- if the \(0\)s and \(1\)s already tell us the correct column, but the incorrect row, flip the coin of the top right box; and
- if the \(0\)s and \(1\)s tell us the wrong row and the wrong column (like in our example), then we flip the coin of the top left box.
Don't forget to subscribe to the newsletter to get bi-weekly problems sent straight to your inbox and to add your reaction below.
Become a better Python 🐍 developer 🚀
+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!
My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.
