Let's prove that if you want to maximise \(ab\) with \(a + b\) equal to a constant value \(k\), then you want \(a = b = \frac{k}{2}\).
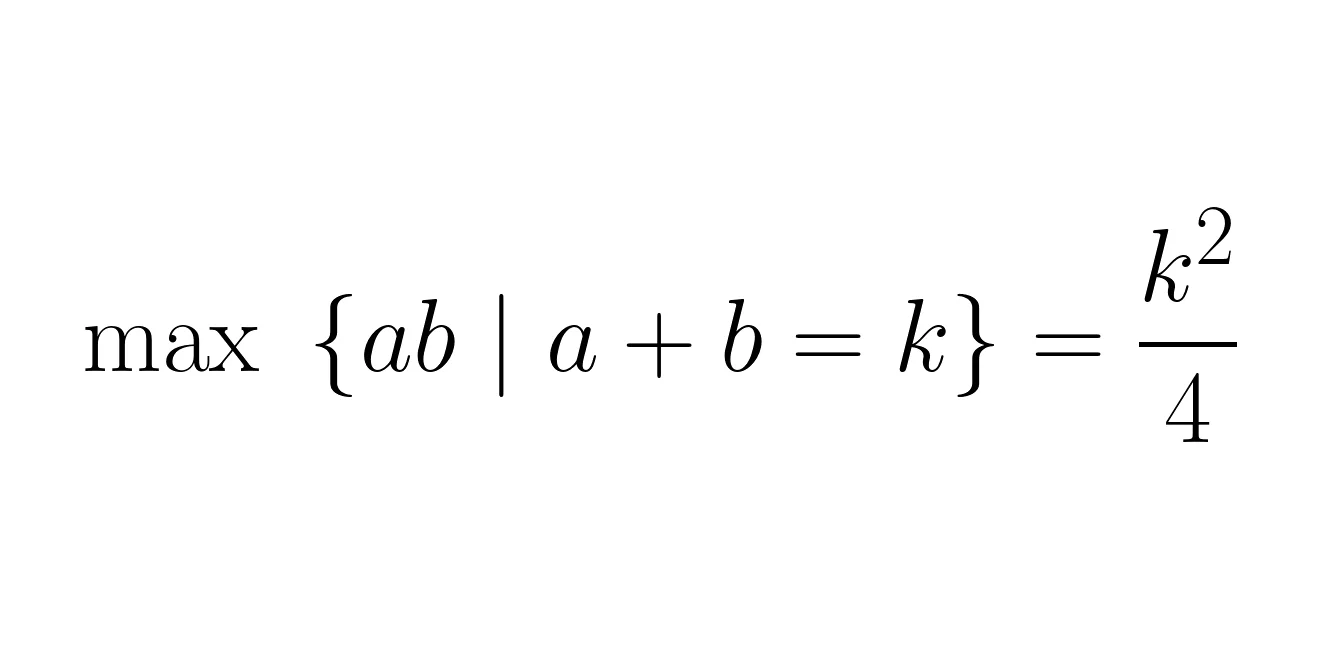
Twitter proof
Twitter proof:
— Mathspp (@mathsppblog) November 5, 2020
Take s = k/2. If a = s+h then b = s-h, from which we get that ab = (s+h)(s-h) = s^2 - h^2. Because we know h^2 >= 0, ab is maximised when h = 0, that is a = b = s = k/2.https://t.co/9ypegSMF2F
Do you have an idea for a twitter proof? Let me know in the comments below!
Become a better Python 🐍 developer 🚀
+35 chapters. +400 pages. Hundreds of examples. Over 30,000 readers!
My book “Pydon'ts” teaches you how to write elegant, expressive, and Pythonic code, to help you become a better developer. >>> Download it here 🐍🚀.
